Просторова діагональ

В прямокутному паралелепіпеді або в магічному кубі, чотири просторові діагоналі — це лінії, які йдуть від кута паралелепіпеду або кубу через його центр до протилежного кута. Ці лінії також називають триагоналі або об'ємні діагоналі.

Графічна побудова просторової діагоналі та її математичних розрахунок за теоремою Піфагора
Лінія AC' (показана синім) — це просторова діагональ, а лінія AC (показана червоним) — поверхнева діагональ

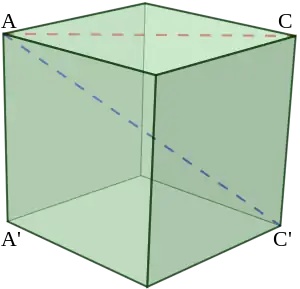
Для того, щоб куб вважався магічним, ці чотири лінії повинні правильно додаватися.

Слово «триагональ» сформоване поєднанням слів «три» та «діагональ», оскільки коли змінна точка рухається по лінії, змінюються три координати. Еквівалент в квадраті — діагональ, оскільки змінюються двоє координат. В тесеракті — це квадрагональ оскільки змінюються четверо координат, і т. д.

Просторова діагональ кубу зі ребром  — .

r-гоналі

Цей розділ стосується переважно магічних гіперкубів.

Математична спільнота почала застосовувати скорочену назву для просторових діагоналей в магічних гіперкубах. Використовуючи r як змінну для опису різних -агоналей, можна скоротити позначання.

Якщо r =

  • 2, це — діагональ, змінюються дві координати;
  • 3, це — триагональ, змінюються дві координати;
  • 4, це — квадрагональ, змінюються дві координати;
  • n = вимір гіперкубу, 2n-1-агоналі повинні правильно додаватися, щоб гіперкуб вважався магічним.

… Відповідно, якщо r =

  • 1, то лінія паралельна поверхні, змінюється лише одна координата. Така лінія може називатися монагоналлю, аналогічно до діагоналі і т. д. Лінії, паралельні поверхням (сторонам) гіперкубу, раніше також називалися i-рядами.

Оскільки префікс пан- означає всі, то коротко характеристики магічного гіперкубу можна назвати:

  • якщо пан-r-агоналі правильно додаються при r = 1 та 2, квадрат магічний пандіагонально;
  • якщо пан-r-агоналі правильно додаються при r = 1 та 3, це пантриагональний магічний куб (еквівалент пандіагонального магічного квадрата).
  • якщо пан-r-агоналі правильно додаються при r = 1 та n, то це магічний куб, незалежно від кількості вимірів.

Довжина r-агоналі в гіперкубі зі стороною (ребром) a дорівнює .

Див. також

Джерела
  • John R. Hendricks, The Pan-3-Agonal Magic Cube, Journal of Recreational Mathematics 5:1:1972, pp 51-54. First published mention of pan-3-agonals
  • Hendricks, J. R., Magic Squares to Tesseracts by Computer, 1998, 0-9684700-0-9, page 49
  • Heinz & Hendricks, Magic Square Lexicon: Illustrated, 2000, 0-9687985-0-0, pages 99,165

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.