Просіювання даних
Просіювання даних (також риболовля серед даних, підгонка даних, р-хакінг) є зловживання аналізом даних з метою пошуку закономірностей, які можуть бути представлені як статистично значущі, таким чином, значно збільшуючи ризик помилковопозитивних результатів. Це робиться шляхом проведення багатьох статистичних тестів на даних і звітності із публікацією лише тих результатів, що мають статистичну значущість. [1]
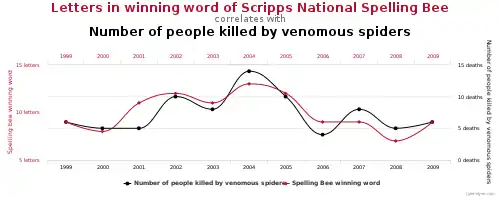
Процес просіювання даних включає перевірку кількох гіпотез з використанням одного набору даних шляхом вичерпного пошуку - або у комбінаціях змінних, які можуть показати кореляцію, або у групах спостережень, які показують різницю середніх значеннь, або в їх розбитті на підгрупи за якимись іншими змінними.
Звичайні тести статистичної значущості базуються на ймовірності виникнення певного результату при однократному експерименті, і обов'язково враховують певний ризик помилок певного типу (помилкові відхилення нульової гіпотези). Цей рівень ризику називається значущістю. Коли проводиться велика кількість тестів, деякі дають хибні результати цього типу. Отже, 5 % випадково обраних гіпотез можуть бути (помилково) статистично значущими на рівні 5 % значущості, 1% можуть (помилково) стати статистично значущими на рівні значущості 1% тощо, і т.д.. Коли перевіряється достатня кількість гіпотез, можна бути впевненим, що деякі з них будуть статистично значущими (навіть якщо це вводить в оману), оскільки майже кожен набір даних із будь-яким ступенем випадковості може містити деякі помилкові кореляції. Якщо це не враховується, результати множинних порівнянь можуть легко ввести в оману дослідників, які використовують методи аналізу даних.
Просіювання даних є прикладом ігнорування проблеми множинного порівняння. Одна з форм - це відсутність у статтях інформації про кількість проведених порівнянь підгруп.[2]
Відбір висновків з даних
Звичайна процедура частотної статистичної перевірки гіпотез полягає в розробці науково-дослідницької гіпотези, такої як «люди з вищих соціальних класів живуть довше», зборі відповідних даних, а потім проведення статистичного тесту значущості, щоб побачити, наскільки велика ймовірність отримання цих даних при однократному дослідженні. Останній крок називається перевіркою нульової гіпотези.
Ключовим моментом у належному статистичному аналізі є перевірка гіпотези за допомогою доказів (даних), які не використовувались при побудові гіпотези. Це критично важливо, оскільки кожен набір даних містить деякі закономірності, повністю обумовлені випадковістю. Якщо гіпотеза не перевіряється на іншому наборі даних, з тієї самої статистичної сукупності, неможливо оцінити ймовірність того, що така закономірность утворена тільки випадковістю. Див. гіпотези тестування, запропоновані даними .
Ось простий приклад. Кидання монети п’ять разів із результатом 2 орла та 3 решки може призвести до припущення, що монета віддає перевагу решці 3/5 на 2/5. Якщо цю гіпотезу перевірити на існуючому наборі даних, вона підтверджується, але таке підтвердження безглузде. Правильною процедурою було б заздалегідь сформувати гіпотезу про те, яка існує ймовірність випадіння решки, а потім кидати монету декілька разів, щоб перевірити, відхиляється гіпотеза чи ні. Якщо спостерігаються три решки і два орла, може бути сформована ще одна гіпотеза, що ймовірність решки становить 3/5, але вона може бути перевірена лише новим киданням монет. Важливо усвідомити, що статистична значущість при неправильній процедурі є абсолютно помилковою - тести значущості не захищають від просіювання даних.
Гіпотеза, висунута на основі нерепрезентативних даних
Припустимо, що дослідження випадкової вибірки людей включає рівно двох людей з днем народження 7 серпня: Марійки та Івана. Хтось, хто займається просіюванням даних, може спробувати знайти додаткову схожість між Марійкою та Іваном. Беребираючи сотні або тисячі можливих подібностей між ними, кожна з яких має низьку ймовірність бути справжньою, майже напевно можна знайти незвичну подібність. Можливо, Іван та Марійка - єдині двоє людей у дослідженні, які три роки були неповнолітніми у коледжі. Тоді упередженою, внаслідок просіювання даних, гіпотезою може бути: "Люди, народжені 7 серпня, мають набагато більший шанс бути неповнолітніми більше ніж два роки в коледжі".
Самі дані, вирвані з контексту, можуть розглядатися як такі, що сильно підтверджують такий зв'язок, оскільки ніхто з різним днем народження не провів свої три роки неповноліття в коледжі. Однак якщо (як і вірогідно) це хибна гіпотеза, цей результат, швидше за все, не буде відтворюваним; при будь-якій спробі перевірити, чи мають інші люди, народжені 7 серпня, подібну ознаку, швидше за все, майже одразу будуть отримані суперечливі результати.
Упередженість
Упередженість - це систематична помилка в аналізі. Наприклад, лікарі призначали хворим на ВІЛ з високим серцево-судинним ризиком певне лікування ВІЛ - абакавір та пацієнтам з меншим ризиком - інші препарати. Це перешкоджає простій оцінці абакавіру порівняно з іншими методами лікування. Аналіз, без корегування цього упередження, несправедливо дійшов висновку про небезпеку абакавіру, оскільки пацієнти, які його приймали мали більший ризик, тому більшість із них мали серцеві напади. [2] Ця проблема може бути дуже серйозною, наприклад, під час спостережного дослідження . [1]
Пропуски даних, невизначені додаткові фактори та втрата даних спостереження після втручання також можуть призвести до упередженості.[2] Вибираючи статті зі значущим значенням p, не беруться до уваги дослідження з негативними результатами - що є упередженням публікації . Це також відоме як "упередження шафи з файлами", оскільки менш значущі результати p- значення залишаються у картотеці та ніколи не публікуються.
Багаторазове моделювання
Інший аспект впливу знання даних на результати статистичних тестів можна побачити при, при аналізі даних методом лінійної регресії. Вирішальним кроком у цьому процесі є рішення, які коваріати включати у рівняння, яке пояснює одну або кілька інших змінних. Існують як статистичні (поетапна регресія ), так і сенсові міркування, які змушують авторів віддавати перевагу одним із своїх моделей над іншими, і це є ліберальним використанням статистичних тестів. Однак відкинути одну або кілька змінних з рівняння на основі даних означає, що не можна достовірно застосовувати стандартні статистичні процедури до збережених змінних у рівнянні так, як ніби нічого не сталося. Природно, збережені змінні повинні були пройти якусь попередню перевірку (можливо, неточну й інтуїтивну), яку відкинуті перемінні не пройшли. У 1966 р. Селвін і Стюарт порівняли змінні, збережені в моделі, з рибами, які не пройшли крізь сітку - в тому сенсі, що їх ефекти повинні бути більшими, ніж ефекти тих, що проскочили крізь сітку. Це не тільки змінює результати усіх наступних тестів на остаточній пояснювальній моделі, це може внести упередженість та змінити середню квадратичну помилку в оцінці. [3] [4]
Приклади в метеорології та епідеміології
У метеорології гіпотези часто формулюються з використанням даних до теперішнього часу і перевіряються на основі майбутніх метеорологічних даних, що гарантує, що навіть підсвідомо майбутні дані не можуть вплинути на формулювання гіпотези. Звичайно, така дисципліна вимагає очікування появи нових даних, щоб показати прогнозовану силу сформульованої теорії проти нульової гіпотези . Цей процес гарантує, що ніхто не може звинуватити дослідника у ручній підгонці прогностичної моделі до наявних даних, оскільки майбутня погода ще не відома.
В якості іншого прикладу, припустимо, що спостерігачі відзначають, що у певному місті, можливо існує кластер раку, але не має твердої гіпотези, чому це так. Однак вони мають доступ до великої кількості демографічних даних про місто та околиці, що містять виміри сотень або тисяч різних змінних, переважно некорельованих. Навіть якщо всі ці змінні не залежать від рівня захворюваності на рак, велика ймовірність, що принаймні одна змінна суттєво корелює із частотою раку в цій місцевості. Хоча це може слугувати на користь гіпотези, для підтвердження необхідне подальше тестування з використанням тих самих змінних, але з даними з іншої місцевості. Зауважте, що р- значення 0,01 свідчить про те, що у 1 % випадків результат, принаймні, такий екстремальний, буде отриманий випадково; якщо перевіряються сотні або тисячі гіпотез (із взаємно відносно некорельованими незалежними змінними), то, швидше за все, можна отримати р- значення менше 0,01 для багатьох нульових гіпотез.
Засоби захисту
Шукати закономірності в даних є правомірним. Застосування статистичного аналізу до тих самих даних, з яких випливає закономірність, є неправильним. Одним із способів побудови гіпотез, уникаючи просіювання даних, є проведення рандомізованих вибіркових тестів . Дослідник збирає набір даних, а потім випадковим чином розподіляє його на дві підмножини A і B. Тільки одна підмножина - скажімо, підмножина A - досліджується для створення гіпотез. Після того, як гіпотеза сформульована, вона повинна бути перевірена на підмножині B, яка не була використана для побудови гіпотези. Тільки тоді, коли дані з підмножини В також підтримують цю гіпотезу, є розумним вважати, що гіпотеза може бути справедливою. (Це простий тип перехресної перевірки, який часто називають навчальним тестом або валідацією з розділеною половиною. )
Інший засіб для захисту під просіювання даних - це записати кількість усіх тестів значущості, проведених під час дослідження, і просто розділити рівень значущості («альфа») на це число; такою є корекція Бонферроні . Однак це дуже консервативний спосіб. Загальновідомий альфа-коефіцієнт 0,05, поділений таким чином на 1000, щоб врахувати 1000 тестів значимості, дає дуже сувору альфу 0,00005. Методами, особливо корисними для дисперсійного аналізу та для побудови довірчих інтервалів для регресій, що включають базові функції, є метод Шеффе, а якщо дослідник має на увазі лише попарні порівняння, метод Т'юкі. Використання коефіцієнта хибних відкриттів Бенджаміні та Хохберга є більш складним підходом, який став популярним методом контролю множинних порівнянь.
Можна чітко розділити аналіз даних на підтверджуваний та дослідницький. Висновки, що базуються на статистиці підходять лише для першого з них. [4]
Зрештою, статистична значущість тесту та статистична довірчисть знахідки є спільними властивостями даних і методу, що використовується для дослідження цих даних. Таким чином, якщо хтось каже, що певна подія має ймовірність 20 % ± 2 %, у 19 випадків із 20, це означає, що ймовірність події, оцінена саме тим методом, який використовувався, знаходиться між 18 % та 22 % з імовірністю 0,95. Жодна заява про статистичну значущість не може бути проголошена без належного врахування методу, що використовується для оцінки даних.
Академічні журнали дедалі частіше переходять до практики передзаявленого звіту, який має на меті протидіяти дуже серйозним проблемам, таким як просіювання даних та <abbr about="#mwt47" data-mw="{"parts":[{"template":{"target":{"wt":"abbr","href":"./Template:Abbr"},"params":{"1":{"wt":"HARKing"},"2":{"wt":"Hypothesizing After Results are Known"}},"i":0}}]}" data-ve-no-generated-contents="true" id="mwcg" title="Hypothesizing After Results are Known" typeof="mw:Transclusion mw:ExpandedAttrs">HARKing</abbr>, які зробили дослідження з тестування гіпотез дуже ненадійними: наприклад, журнал Nature Human Behaviour перейшов на передзаявлений звіт, оскільки він “переносить [акценти] з результатів дослідження на питання, якими керується дослідження, та методи, що використовуються для відповіді на них”. [5] European Journal of Personality визначає цей формат таким чином: «У передзаявленому звіті автори створюють пропозицію дослідження, яка включає теоретичні та емпіричні передумови, дослідницькі питання / гіпотези та пілотні дані (якщо такі є). Після надходження до редакції ця пропозиція буде розглянута до початку збору даних, і якщо вона буде прийнята, стаття, отримана в після цієї рецензованої процедури, буде опублікована незалежно від результатів дослідження ". [6]
Загальнодоступність методів та результатів дослідження за принципом відкритої науки ще більше ускладнює використання прийому просіювання даних. [7]
Список літератури
- Davey Smith, G.; Ebrahim, S. (2002). Data dredging, bias, or confounding. BMJ 325 (7378): 1437–1438. PMC 1124898. PMID 12493654. doi:10.1136/bmj.325.7378.1437.
- Young, S. S.; Karr, A. (2011). Deming, data and observational studies. Significance 8 (3): 116–120. doi:10.1111/j.1740-9713.2011.00506.x.
- Selvin, H.C.; Stuart, A. (1966). Data-Dredging Procedures in Survey Analysis. The American Statistician 20 (3): 20–23. JSTOR 2681493. doi:10.1080/00031305.1966.10480401.
- Berk, R.; Brown, L.; Zhao, L. (2009). Statistical Inference After Model Selection. J Quant Criminol 26 (2): 217–236. doi:10.1007/s10940-009-9077-7.
- Promoting reproducibility with registered reports. Nature Human Behaviour 1 (1): 0034. 10 січня 2017. doi:10.1038/s41562-016-0034.
- Streamlined review and registered reports soon to be official at EJP. ejp-blog.com.
- Vyse, Stuart (2017). P-Hacker Confessions: Daryl Bem and Me. Skeptical Inquirer 41 (5): 25–27. Архів оригіналу за 5 серпня 2018. Процитовано 5 серпня 2018.
Додаткова література
- Ioannidis, John P.A. (30 серпня 2005). Why Most Published Research Findings Are False. PLOS Medicine (San Francisco: Public Library of Science) 2 (8): e124. ISSN 1549-1277. PMC 1182327. PMID 16060722. doi:10.1371/journal.pmed.0020124.
- Head, Megan L.; Holman, Luke; Lanfear, Rob; Kahn, Andrew T.; Jennions, Michael D. (13 березня 2015). The Extent and Consequences of P-Hacking in Science. PLOS Biology 13 (3): e1002106. PMC 4359000. PMID 25768323. doi:10.1371/journal.pbio.1002106.
- Insel, Thomas (14 листопада 2014). P-Hacking. NIMH Director's Blog (англ.).
- Smith, Gary (2016). Standard Deviations: Flawed Assumptions, Tortured Data, and Other Ways to Lie with Statistics. Gerald Duckworth & Co. ISBN 9780715649749.