Рамковий граф
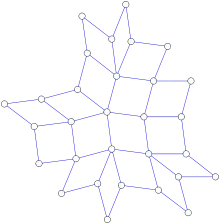
У теорії графів рамковим графом називають вид неорієнтованого графу, який можна намалювати на площині таким способом, що будь-яка обмежена грань є чотирикутником і будь-яка вершина з трьома і менше сусідами інцидентна необмеженій грані.
Пов'язані класи графів
Окремими випадками рамкових графів є дерева, решітки, шестірні і графи поліміно.
Оскільки рамкові графи планарні, вони також є медіанними, що означає, що для будь-яких трьох вершин u, v і w існує єдина вершина m(u,v,w) (називана медіаною), яка лежить на найкоротшому шляху між кожною парою цих трьох вершин[1]. Як і у випадку загальніших медіанних графів, рамкові графи є частковими кубами - їх вершини можна позначити бітовими рядками так, що відстань Геммінга між рядками дорівнюватиме найкоротшій відстані між вершинами.
Характеристика

Рамкові графи можна схарактеризувати кількома способами, відмінними від властивості планарності[2]:
- Вони є медіанними графами, що не містять породженим підграфом будь-якого члена нескінченного сімейства заборонених графів. До цих заборонених графів належать куб (симплекс-граф K3), прямий добуток ребра і клешні K1,3 (симплекс-граф клешні) і графи, утворені зі шестерні додаванням вершини, з'єднаної ребром з центром колеса.
- Вони є зв'язними і двочастковими графами такими, що якщо вибрати будь-яку вершину r як корінь, то будь-яка вершина має максимум два сусіди, що містяться ближче до r, і такі, що для будь-якої вершини v зв'язка вершини v (граф, що складається з вершин для кожного інцидентного v ребра і ребер для всіх циклів довжини 4, що містять вершину v) є або циклом довжини не менше трьох, або незв'язним набором шляхів.
- Вони є двоїстими графами конфігурацій прямих на гіперболічній площині, в яких немає трьох попарно перетинних прямих.
Алгоритми
Опис рамкових графів у термінах відстані від кореня і зв'язок вершин (див. вище) можна використати разом з пошуком у ширину як частину алгоритму з лінійним часом роботи для перевірки, чи є даний граф рамковим без необхідності використовувати складніші алгоритми з лінійним часом роботи для перевірки планарності довільних графів[2].
Деякі алгоритмічні задачі на рамкових графах можна розв'язати ефективніше, ніж ті самі задачі для загальніших планарних графів. Наприклад, Чепой, Драган, Ваксес і Фансілліні[3][4] запропонували лінійні за часом алгоритми обчислення діаметра рамкових графів і для пошуку вершини, розташованої на мінімальній відстані від усіх інших вершин (тобто вершини, на якій досягається мінімум максимальної відстані до всіх інших вершин).
Примітки
- Солтан, Замбицкий, Присакару, 1973. Див. загальніше обговорення планарних медіанних графів у Петеріна (Peterin, 2006).
- Bandelt, Chepoi, Eppstein, 2010.
- Chepoi, Dragan, Vaxès, 2002.
- Chepoi, Fanciullini, Vaxès, 2004.
Література
- H.-J. Bandelt, V. Chepoi, D. Eppstein. Combinatorics and geometry of finite and infinite squaregraphs // SIAM Journal on Discrete Mathematics. — 2010. — Т. 24, вип. 4 (9 листопада). — С. 1399—1440. — arXiv:0905.4537. — DOI:.
- V. Chepoi, F. Dragan, Y. Vaxès. Proc. 13th Annu. ACM–SIAM Symp. on Discrete Algorithms (SODA 2002). — 2002. — 9 листопада. — С. 346–355.
- V. Chepoi, C. Fanciullini, Y. Vaxès. Median problem in some plane triangulations and quadrangulations // Comput. Geom.. — 2004. — Т. 27, вип. 3 (9 листопада). — С. 193—210. — DOI:.
- I. Peterin. A characterization of planar median graphs // Discussiones Mathematicae Graph Theory. — 2006. — Т. 26 (9 листопада). — С. 41—48.[недоступне посилання з березня 2018]
- Солтан П. С., Замбицкий Д. К., Присакару К. Ф. Экстремальные задачи на графах и алгоритмы их решения. — Chişinǎu, Moldova : Штиинца, 1973. — 9 листопада.