Раціональна функція

Раціональна функція однієї змінної — це алгебраїчний вираз, що є відношенням двох многочленів, тобто має вигляд

{\frac {P(x)}{Q(x)}}={\frac {a_{n}x^{n}+\ldots +a_{1}x+a_{0}}{b_{m}x^{m}+\ldots +b_{1}x+b_{0}}}.

При цьому коефіцієнти многочленів належать деякому заздалегідь визначеному полю, наприклад, множині дійсних або комплексних чисел. Причому коефіцієнти зовсім не обов'язково мають бути раціональними числами.

Степенем раціональної функції називається максимум з степенів многочленів P та Q. Раціональні функції степеня 1 називаються перетворенням Мебіуса.

Раціональна функція визначена для всіх значень змінних, крім тих, при яких знаменник перетворюється в нуль.

Функції, які неможливо представити у вигляді відношення двох многочленів, називають ірраціональними функціями.

На раціональні функції поширюються арифметичні дії (додавання, множення, віднімання і ділення). Сукупність усіх раціональних функцій сама утворює поле, так зване поле раціональних функцій. Раціональні функції належать до ширшого класу елементарних функцій.

Так само визначаються раціональні функції кількох змінних

R(x)={\frac {P_{n}(x_{1},\dots ,x_{n})}{Q_{m}(x_{1},\dots ,x_{m})}}

Властивості

Будь-який вираз, який можна отримати зі змінних $x_{1},\dots ,x_{n}$ за допомогою чотирьох арифметичних дій, є раціональною функцією.
Множина раціональних функцій замкнута щодо арифметичних дій і операції композиції.
Будь-яка раціональна функція може бути представлена у вигляді суми найпростіших дробів (див. Метод невизначених коефіцієнтів), це застосовується при аналітичному інтегруванні.

Приклади

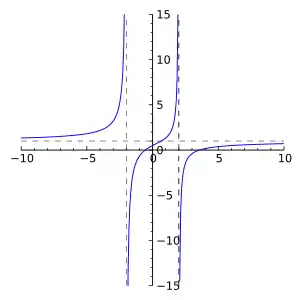
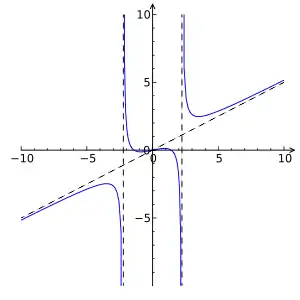
Приклади раціональних функцій

Раціональна функція степеня 2:

y={\frac {x^{2}-3x-2}{x^{2}-4}}

Раціональна функція степеня 3:

y={\frac {x^{3}-2x}{2(x^{2}-5)}}

Раціональна функція

f(x)={\frac {x^{3}-2x}{2(x^{2}-5)}}

не визначена при

x^{2}=5\Leftrightarrow x=\pm {\sqrt {5}}

.

Раціональна функція

f(x)={\frac {x^{2}+2}{x^{2}+1}}

визначена на всіх дійсних числах, але не на всіх комплексних числах. Невизначеність виникає коли x є квадратним коренем з

-1

(т.з.

i

- уявна одиниця або

-i

), коли виникає ділення на нуль:

f(i)={\frac {i^{2}+2}{i^{2}+1}}={\frac {-1+2}{-1+1}}={\frac {1}{0}}

.

Раціональна функція

f(x)={\frac {x^{3}-2x}{2(x^{2}-5)}}

, при x що прямує до нескінченності, прямує до

{\frac {x}{2}}

.

Функція-константа, наприклад f(x) = π є раціональною функцією тому що константа є многочленом (виродженим). Зауваження. Функція є раціональною навіть коли f(x) є ірраціональним числом при всіх x.

Раціональна функція

f(x)={\frac {x}{x}}

дорівнює 1 для всіх x крім 0, що є усувною особливою точкою.

Література

Г.М. Фіхтенгольц «Курс диференціального та інтегрального числення», Т I, Москва 1966.

Дивись також

Алгебраїчні функції

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.