Ромбоікосододекаедр

Ромбоікосододека́едр[1][2][3] — напівправильний багатогранник, який складається з 12 правильних п'ятикутників, 30 квадратів і 20 трикутників, архімедове тіло. Має ікосаедричний тип симетрії. В кожній з вершин сходяться трикутник, п'ятикутник і 2 квадрати.

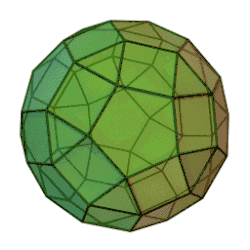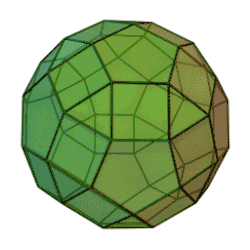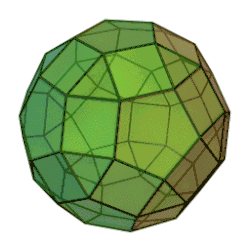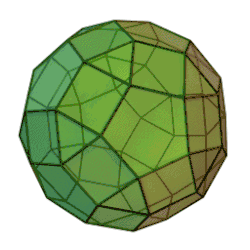
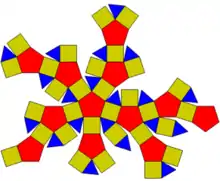
Ромбоікосододекаедр
Розгортка ромбоікосододекаедра
Тривимірна модель ромбоікосододекаедра

Ромбоікосододекаедр можна подати як додекаедр, зрізаний за вершинами і ребрами (при цьому трикутники відповідають вершинам додекаедра, а квадрати — ребрам), або як ікосаедр, зрізаний так само (при цьому п'ятикутники відповідають вершинам ікосаедра, а квадрати — ребрам), або ж як зрізаний ікосододекаедр, чим він по суті і є.

Декартові координати

Декартові координати вершин ромбоікосододекаедра з довжиною ребра 2 із центром у початку координат є парними перестановками з:[4]

(± 1, ± 1, ± φ 3),
(± φ 2, ± φ, ± 2 φ),
(± (2+ φ), 0, ± φ 2), де φ = 1 + √52 являє собою золотий перетин . Отже, радіус описаної сфери цього ромбоікосододекаедра дорівнює відстані цих точок від початку координат, а саме √φ6+2 = √8φ+7 для довжини ребра 2. Для одиничної довжини ребра, зменшивши R удвічі, маємо
R = √8φ+72 = √11+4√52 ≈ 2,233.

Ортогональні проєкції
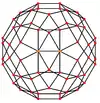
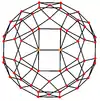
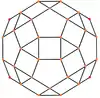
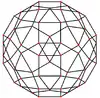
Ортогональна проєкція в Геометрії (1543) Августина Гіршфоґеля

Ромбоікосододекаедр має шість особливих ортогональних проєкцій, центрованих на вершині, на ребрах двох типів і гранях трьох типів: трикутнику, квадраті та п'ятикутнику. Останні дві відповідають площинам Коксетера А2 і Н2.

Ортогональні проєкції
У центрі Вершина Ребро

3-4

 Ребро

5-4

 Квадратна грань Трикутна грань П'ятикутна грань
Суцільна
Каркасна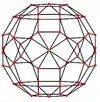
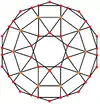Проєктивна

симетрія

 [2] [2] [2] [2] [6] [10]
Дуальне

зображення

Сферична мозаїка

Ромбоікосододекаедр також можна зобразити у вигляді сферичної мозаїки та проєктувати на площину за допомогою стереографічної проєкції . Ця проєкція є конформною, зберігаючи кути, але не площі та довжини. Прямі лінії на кулі проєктуються на площину як дуги кола.


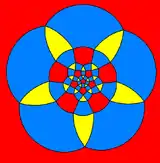У центрі —п'ятикутник
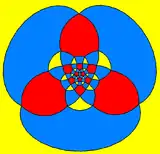У центрі — трикутник
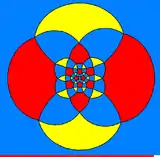У центрі — квадрат
Ортогональна проєкція Стереографічні проєкції

Примітки
  1. Веннинджер, 1974, с. 20, 38.
  2. Энциклопедия элементарной математики, 1963, с. 437, 435.
  3. Люстерник, 1956, с. 184.
  4. Weisstein, Eric W. Icosahedral group(англ.) на сайті Wolfram MathWorld.

Література
  • М. Веннинджер. Модели многогранников. — Мир, 1974.
  • Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова, А. И. Маркушевича, А. Я. Хинчина. — М. : Государственное издательство физико-математической литературы, 1963. — С. 382-447.
  • Л. А. Люстерник. Выпуклые фигуры и многогранники. — М. : Государственное издательство технико-теоретической литературы, 1956.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.