Рівняння Бете — Солпітера
Рівняння Бете — Солпітера (назване на честь Ганса Бете та Едвіна Солпітера)[1] описує зв'язані стани квантовопольової системи двох тіл (частинок) у рамках релятивістськи інваріантного формалізму. Першим рівняння опублікував у 1950-му Йоїтіро Намбу, але не навів доведення.[2]
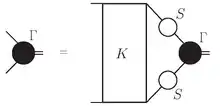
Через загальність та застосування в численних підрозділах теоретичної фізики рівняння Бете-Солпітера має багато різних форм. Форма, що часто використовується у фізиці високих енергій, має вигляд
де Γ — амплітуда Бете-Солпетера, K — взаємодія, а S — пропагатори двох частинок.
У квантовій теорії зв'язані стани живуть нескінченно довго (інакше їх називають резонансами), тому складові взаємодіють нескінченну кількість разів. У підсумку, за нескінченну кількість разів між двома частинками реалізуються усі можливі взаємодії, а рівняння Бете-Солпітера є інструментом для розрахунку властивостей зв'язаних станів. Розв'язок цього рівняння, амплітуда Бете-Солпітера, описує зв'язаний стан, що є предметом інтересу.
Оскільки його можна вивести, ідентифікуючи зв'язані стани з полюсами S-матриці, його можна зв'язати з квантовим описом процесів розсіяння і функцією Гріна.
Рівняння Бете-Солпітера — загальний інструмент квантової теорії поля, тож воно зустрічається у будь-якій квантовопольовій теорії. Прикладами можуть слугувати позитроній (зв'язаний стан електрон-позитронної пари), екситони (зв'язаний стан електрона і дірки[3]) та мезони (зв'язаний стан кварка й антикварка).[4]
Навіть для простих систем, таких як позитроній рівняння не розв'язується точно, хоча в принципі його можна сформулювати точно. Класифікацію станів можна провести без точного розв'язку. Якщо одна з частинок значно масивніша за іншу, задача значно спрощується, оскільки зводиться до рівняння Дірака для легшої частинки в зовнішньому потенціалі важчої частинки.
Вивід
Вихідним пунктом виводу рівняння Бете-Солпітера є двочастинкове (чотириточкове) рівняння Дайсона
в імпульсному просторі. Тут "G" — двочастинкова функція Гріна , "S" — вільні попагатори, а "K" — ядро взаємодії, в якому містяться всі можливі взаємодії між двома частинками. Тепер важливим кроком є припущення про те, що зв'язані стани проявляються як полюси функції Гріна. Припускається, що дві частинки сходяться й утворюють зв'язаний стан із масою "M", цей зв'язаний стан розповсюджується вільно, а потім знову розпадається на дві складові. Таким чином, вводиться хвильова функція Бете-Солпітера , що є перехідною амплітудою двох складових у зв'язаний стан , а тоді утворює анзац для функції Гріна поблизу полюса у формі
де P — повний імпульс системи. Очевидно, якщо для цього імпульсу виконується , а це співвідношення між енергією та імпульсом у теорії відносності (де 4-імпульс та ), чотириточкова функція Гріна має полюс. Якщо підставити цей анзац у рівняння Дайсона і задати повний імпульс "P" так, щоб виконувалося релятивістське співвідношення між енергією та імпульсом, полюс виникає по обидва боки від знаку рівності.
Порівняння лишків дає:
Це вже рівняння Бете-Солпітера, записане через хвильову функцію Бете-Солпітера. Щоб отримати наведену вище формулу треба ввести амплітуду Бете-Солпітера "Γ"
і оримати
що й записано вище з явною залежністю від імпульсу.
Наближення веселки-східців
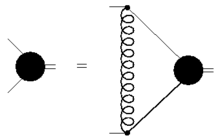
У принципі ядро K містить усі можливі незвідні двочастинкові взаємодії, що можуть статися між двома складовими. Тож, для практичних розрахунків необхідно моделювати взаємодію, вибираючи тільки підмножину взаємодій. Як і в квантовій теорії поля, взаємодія описується через обмін частинками (наприклад, фононами в квантовій електродинаміці або глюонами в квантовій хромодинаміці), найпростіша взаємодія зводиться до тільки одної такої силової частинки.
Оскільки рівняння Бете-Солпітера підсумовує взаємодію нескінченне число разів, відповідна діаграма Фейнмана має вигляд східців (веселки).
Тоді як у квантовій електродинаміці наближення східців призводить до проблем з перехресною симетрією та калібрувальною інваріантністю, а тому вимагає включення перехресних східцевих членів, у квантовій хромодинаміці це наближення доволі часто використовується феноменологічно для розрахунку мас адронів[4], оскільки воно зберігає порушення хіральної симетрії, а тому є важливим внеском у генерацію цих мас.
Нормування
Як для будь-якого однорідного рівняння, розв'язок рівняння Бете-Солпітера визначений тільки з точністю до множника. Цей множник потрібно уточнити, накладаючи певні умови нормування. Для амплітуд Бете-Солпітера це зазвичай означає вимогу збереженння ймовірності (аналогічно нормуванню квантмеханічної хвильової функції), що відповідає рівнянню[5]
Нормування заряду та тензора енергії-імпульсу зв'язаного стану веде до того ж рівняння. У східцевому наближенні ядро взаємодії не залежить від повного імпульсу амплітуди Бете-Солпітера, а тому, у цьому випадку другий член умови нормування зникає.
Див. також
- ABINIT
- Поправка Аракі-Зухера
- Рівняння Брейта
- Рівняння Ліппманна — Швінгера
- Рівняння Швінгера
- Рівняння Дірака для двох тіл
- YAMBO
Посилання
- H. Bethe, E. Salpeter (1951). A Relativistic Equation for Bound-State Problems. Physical Review 84 (6): 1232. Bibcode:1951PhRv...84.1232S. doi:10.1103/PhysRev.84.1232.
- Y. Nambu (1950). Force Potentials in Quantum Field Theory. Progress of Theoretical Physics 5 (4): 614. doi:10.1143/PTP.5.614. Проігноровано невідомий параметр
|doi-access=(довідка) - M. S. Dresselhaus (2007). Exciton Photophysics of Carbon Nanotubes. Annual Review of Physical Chemistry 58: 719. Bibcode:2007ARPC...58..719D. doi:10.1146/annurev.physchem.58.032806.104628.
- P. Maris and P. Tandy (2006). QCD modeling of hadron physics. Nuclear Physics B 161: 136. Bibcode:2006NuPhS.161..136M. arXiv:nucl-th/0511017. doi:10.1016/j.nuclphysbps.2006.08.012.
- N. Nakanishi (1969). A general survey of the theory of the Bethe–Salpeter equation. Progress of Theoretical Physics Supplement 43: 1–81. Bibcode:1969PThPS..43....1N. doi:10.1143/PTPS.43.1. Проігноровано невідомий параметр
|doi-access=(довідка)
Література
Many modern quantum field theory textbooks and a few articles provide pedagogical accounts for the Bethe–Salpeter equation's context and uses. See:
- W. Greiner, J. Reinhardt (2003). Quantum Electrodynamics (вид. 3rd). Springer. ISBN 978-3-540-44029-1.
- Z.K. Silagadze (1998). «Wick–Cutkosky model: An introduction». arXiv:hep-ph/9803307.
Still a good introduction is given by the review article of Nakanishi
- N. Nakanishi (1969). A general survey of the theory of the Bethe–Salpeter equation. Progress of Theoretical Physics Supplement 43: 1–81. Bibcode:1969PThPS..43....1N. doi:10.1143/PTPS.43.1. Проігноровано невідомий параметр
|doi-access=(довідка)
For historical aspects, see
- E.E. Salpeter (2008). Bethe–Salpeter equation (origins). Scholarpedia 3 (11): 7483. Bibcode:2008SchpJ...3.7483S. arXiv:0811.1050. doi:10.4249/scholarpedia.7483.
Посилання
- BerkeleyGW — метод псевдопотенціалу для плоских хвиль
- ExC — плоскі хвилі
- Fiesta — Gaussian all-electron method