Сателітний вузол
В математичній теорії вузлів сателітний вузол — це вузол, що містить у своєму доповненні нестисний, тор, що не є ∂-паралельним[1]. Кожен вузол є або гіперболічним, або торичним, або сателітним. До класу сателітних вузлів належать складені вузли, кабельні вузли та дублі Вайтгеда. (Див. означення останніх двох класів нижче в розділі Основні сімейства). Сателітне зачеплення — це зачеплення, яке обертається навколо супровідного вузла K в тому сенсі, що воно лежить усередині його регулярного околу[2].
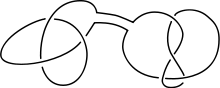
Сателітний вузол можна наочно описати так: візьміть нетривіальний вузол , що лежить всередині незавузленого повнотора . Тут «нетривіальний» означає, що вузол не може лежати в 3-сфері, яка міститися у і не може бути ізотопним центральній кривій суцільного тора. Потім повнотор зав'яжіть у нетривіальний вузол.

Це означає, що існує нетривіальне вкладення і . Центральна крива повнотора переходить на вузол , який називається «супровідним вузлом»[3] і грає роль планети, навколо якої облітає «сателітний вузол» . Побудова гарантує, що — не ∂-паралельний нестисливий тор у доповненні до . Складені вузли містять особливий вид нестисного тора — охопно-ковзний[уточнити] (англ. swallow-follow torus) — який охоплює один доданок та проходить уздовж іншого.
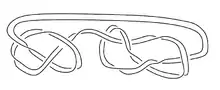
Якщо — незавузлений повнотор, то є трубчастим околом безвузла . Двокомпонентне з'єднання разом із вкладенням називається шаблоном, пов'язаним із сателітною операцією.
Домовленість: зазвичай вимагається, що вбудовування розкручене в тому сенсі, що необхідно надіслати стандартну довготу до стандартної довготи . Іншими словами, для будь-яких двох неперетинних кривих , зберігає їхні числа зв'язків, тобто: .
Основні сімейства
Якщо — торичний вузол, то називають кабельним вузлом. Приклади 3 і 4 є кабельними вузлами.
Якщо — нетривіальний вузол в і якщо диск стиснення для перетинає рівно в одній точці, то називають сумою підключення. Іншими словами, візерунок є сумою нетривіального вузла з зачеплення Хопфа.
Якщо зачеплення — зачеплення Вайтгеда, то називають дублем Вайтгеда. Якщо розкручений, називають розкрученим дублем Вайтгеда.
Приклади
Приклад 1: Сума з'єднання вузла-вісімки і трилистника.
Приклад 2: Розкручений дубль Вайтгеда вісімки.
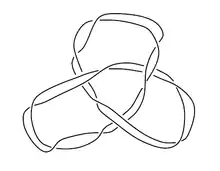
Приклад 3: Кабельна сума.
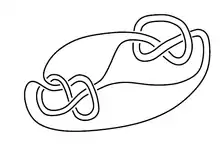
Приклад 4: Кабельний трилисник.
Приклади 5 і 6 є варіантами однієї конструкції. Обидва вони мають у своїх доповненнях два непаралельних, не ∂-паралельних нестисливих тори, що розбивають доповнення на об'єднання трьох многовидів. У прикладі 5 ці многовиди: доповнення кілець Борромео, доповнення трилисника та доповнення вісімки. У прикладі 6 доповнення до вісімки замінено ще одним доповненням трилисника.
Походження
1949 року[4] Горст Шуберт довів, що кожен орієнтований вузол в розкладається як сума простих вузлів унікальним способом, аж до переупорядкування, роблячи моноїд орієнтованих ізотопічних класів вузлів у вільним комутативним моноїдом на зліченно-нескінченній кількості твірних. Незабаром після цього він зрозумів, що може надати нове доведення своєї теореми шляхом ретельного аналізу нестисливих торів, присутніх у доповненні суми. Це привело його до вивчення нестисливих торів у доповненнях вузлів у його відомій роботі Knoten und Vollringe[5], де він визначив сателітні та супровідні вузли.
Подальші роботи
Демонстрація Шубертом того, що нестисливі тори відіграють важливу роль у теорії вузлів, була однією з ранніх ідей, що привели до об'єднання теорії 3-многовидів і теорії вузлів. Це привернуло увагу Вальдгаузена, який пізніше використав нестисливі поверхні, щоб показати, що великий клас 3-многовидів гомеоморфний тоді і тільки тоді, коли їхні фундаментальні групи ізоморфні.[6] Вальдгаузен припустив розклад 3-многовидів уздовж сфер і нестисливих торів, відомий зараз як розклад 3-многовидів Жако — Шалена — Йогансона. Пізніше це стало основним компонентом розвитку геометризації, яку можна розглядати як часткову класифікацію 3-вимірних многовидів. Відгалуження теорії вузлів вперше описано в довго не публікованому рукописі Бонахона і Зібенмана[7].
Унікальність сателітної декомпозиції
У роботі Knoten und Vollringe Шуберт довів, що в деяких випадках існує по суті унікальний спосіб подати вузол як сателітний. Але є також багато відомих прикладів, коли розклад не є унікальним[8]. З належним чином розширеним поняттям сателітної операції, що називається сплайсингом, розклад Жако — Шалена — Йогансона дає відповідну теорему унікальності для сателітних вузлів.[9][10]
Див. також
Примітки
- Colin Adams, The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots, (2001), ISBN 0-7167-4219-5
- Переклад "regular neighborhood" у словнику. Процитовано 3 березня 2021.
- Переклад "companion knot" у словнику. Процитовано 3 березня 2021.
- Schubert, H. Die eindeutige Zerlegbarkeit eines Knotens in Primknoten. S.-B Heidelberger Akad. Wiss. Math.-Nat. Kl. 1949 (1949), 57–104.
- Schubert, H. Knoten und Vollringe. Acta Math. 90 (1953), 131—286.
- Waldhausen, F. On irreducible 3-manifolds which are sufficiently large.Ann. of Math. (2) 87 (1968), 56–88.
- F.Bonahon, L.Siebenmann, New Geometric Splittings of Classical Knots, and the Classification and Symmetries of Arborescent Knots,
- Motegi, K. Knot Types of Satellite Knots and Twisted Knots. Lectures at Knots '96. World Scientific.
- Eisenbud, D. Neumann, W. Three-dimensional link theory and invariants of plane curve singularities. Ann. of Math. Stud. 110
- Budney, R. JSJ-decompositions of knot and link complements in S³. L'enseignement Mathematique 2e Serie Tome 52 Fasc. 3–4 (2006). arXiv: math.GT/0506523