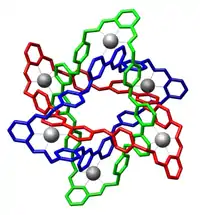
Кільця Борромео

Кільця Борромео[1] — зачеплення, що складається з трьох топологічних кіл, які зчеплені і утворюють бруннове зачеплення (тобто видалення будь-якого кільця призведе до роз'єднання двох інших). Іншими словами, ніякі два з трьох кілець не зчеплені, як в зачепленні Хопфа, проте, всі разом вони зчеплені.

Математичні властивості

Попри позірну з ілюстрацій природність кілець Борромео, з геометрично ідеальних кіл таке зачеплення зробити неможливо[2]. Також це можна побачити, розглянувши діаграму вузла: якщо припустити, що кола 1 та 2 дотикаються в двох точках перетину, то вони лежать або в одній площині, або на сфері. В обох випадках третє коло має перетинати цю площину чи сферу в чотирьох точках і не лежати на ній, що неможливо[3].

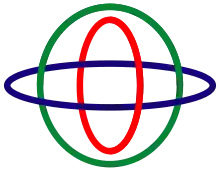
Реалізація кілець Борромео у вигляді еліпсів
Тривимірне подання кілець Борромео

Разом з тим, подібне зачеплення можна здійснити з використанням еліпсів, причому ексцентриситет цих еліпсів можна зробити як завгодно малим. З цієї причини тонкі кільця, зроблені з гнучкого дроту можна використовувати як кільця Борромео.

Зачеплення

В теорії вузлів кільця Борромео є найпростішим прикладом бруннового зачеплення — хоча будь-яка пара кілець не зчеплена, їх не можна роз'єднати.

Найпростіший спосіб це довести — розглянути фундаментальну групу доповнення двох незчеплених кіл; за теоремою Зейферта — ван Кампена це вільна група з двома твірними, a і b, а тоді третьому циклу відповідає клас комутатора, [a, b] = aba−1b−1, що можна бачити з діаграми зачеплення. Цей комутатор нетривіальний у фундаментальній групі, а тому кільця Борромео зчеплені.

В арифметичній топології існує аналогія між вузлами і простими числами, що дозволяє простежувати зв'язки простих чисел. Трійка простих чисел (13, 61, 937) є пов'язаною за модулем 2 (її символ Редеї дорівнює -1), але попарно за модулем 2 ці числа не пов'язані (всі символи Лежандра дорівнюють 1). Такі прості називаються «правильними трійками Борромео за модулем 2»[4] або «простими Борромео за модулем 2».[5]

Гіперболічна геометрія

Кільця Борромео є прикладом гіперболічного зчеплення — доповнення кілець Борромео в 3-сфері допускає повну гіперболічну метрику зі скінченним об'ємом. Канонічний розклад (Епштейна — Пеннера) доповнення складається з двох правильних октаедрів. Гіперболічний об'єм дорівнює 16Л(π/4) = 7.32772…, де Л — функція Лобачевського.[6]

Зв'язок з косами
Стандартна коса з трьох стрічок відповідає кільцям Борромео.

Якщо розсікти кільця Борромео, отримаємо одну ітерацію звичайного плетіння коси. І навпаки, якщо зв'язати кінці (однієї ітерації) звичайної коси, отримаємо кільця Борромео. Видалення одного кільця звільняє два інших, і видалення однієї стрічки з коси звільняє дві інші — вони є найпростішими брунновим зачепленням і брунновою косою відповідно.

У стандартній діаграмі зачеплення кільця Борромео упорядковані в циклічному порядку. Якщо використовувати кольори, як вище, червоне буде лежати над зеленим, зелене над синім, синє над червоним, і при видаленні одного з кілець одне з решти буде лежати над іншим і вони виявляться незачепленими. Так само і з косою: кожна стрічка лежить над другою і під третьою.

Історія
Валкнут на Стура-Хаммарському камені
Кільця Борромео як символ християнської Трійці з рукописів XIII століття.
Вузол мавпячий кулак.
«Мандала» дискордаіанства, що містить п'ять кілець Борромео.

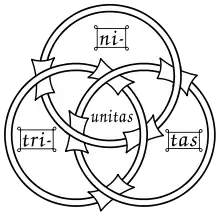
Назву «кільця Борромео» з'явилася через використання їх на гербі аристократичної родини Борромео в північній Італії. Зачеплення значно старше і з'являлося у вигляді валкнута на картинних каменях вікінгів, які датуються сьомим століттям.

Кільця Борромео використовувалися в різних контекстах, таких як релігія і мистецтво, для того щоб показати силу єдності. Зокрема кільця використовувались як символ Трійці. Відомо, що психоаналітик Жак Лакан знайшов натхнення в кільцях Борромео як моделі топології людської особистості, в якій кожне кільце відповідає фундаментальному компоненту реальності («дійсне», «уявне» і «символічне»).

2006 року Міжнародний математичний союз прийняв рішення використати логотип, заснований на кільцях Борромео, для XXV міжнародного конгресу математиків у Мадриді, Іспанія[7].

Кам'яний стовп у храмі Марундіїсварар у Ченнаї, Тамілнад, Індія, датований шостим століттям, містить таку фігуру[8][9].

Часткові кільця

Відомо багато візуальних знаків, що належать до середньовіччя і часів ренесансу, що складаються з трьох елементів, зчеплених один з одним тим самим способом, що й кільця Борромео (в загальноприйнятому двовимірному поданні), але індивідуальні елементи при цьому не є замкнутими кільцями. Прикладами таких символів є роги на снолделевському камені і півмісяці Діани де Пуатьє. Прикладом знаку з трьома різними елементами є емблема клубу Інтернасьонал. Хоч і меншою мірою, до цих символів відносяться ганкиїл і діаграма Венна з трьох елементів.

Також вузол «мавпячий кулак», по суті, є тривимірним поданням кілець Борромео, хоча вузол складається з трьох рівнів.

Більша кількість кілець

Деякі з'єднання в теорії вузлів містять множинні конфігурації кілець Борромео. Одне з'єднання такого типу, що складається з п'яти кілець, використовується як символ у дискордіанізмі, засноване на зображенні з книги «Принципія Дискордія».

Реалізації
Кристалічна структура молекулярних кілець Борромео, наведена Стодартом у журналі «Science», 2004, том 304, с. 1308—1312.

Молекулярні кільця Борромео — молекулярні аналоги кілець Борромео, які є механічно зчепленими молекулярними структурами. 1997 року біолог Мао Ченде (Chengde Mao) зі співавторами з Нью-Йоркського університету успішно сконструювали кільця з ДНК[10]. 2003 року хімік Фрейзер Стоддарт зі співавторами з Каліфорнійського університету, використали комплексні сполуки для побудови набору кілець з 18 компонентів за одну операцію[11].

Квантово-механічний аналог кілець Борромео називається ореолом або станом Єфімова (існування таких станів передбачив фізик Віталій Миколайович Єфімов 1970 року). 2006 року дослідницька група Рудольфа Гріма і Ганса-Крістофа Негерля з Інституту експериментальної фізики Інсбруцького університету (Австрія) експериментально підтвердила існування таких станів у ультрахолодному газі атомів цезію і опублікувала відкриття в науковому журналі Nature[12]. Група фізиків під керівництвом Рандалла Гулета (Randall Hulet) в університеті Райса в Х'юстоні отримали той самий результат за допомогою трьох пов'язаних атомів літію і опублікували своє відкриття в журналі Science Express[13]. 2010 року група під керівництвом К. Танака отримала стан Єфімова з нейтронами (нейтронний ореол)[14].

Див. також

Примітки
  1. Назва виниклаа з герба роду Борромео, на якому ці кільця присутні.
  2. Freedman-Skora, 1987.
  3. Lindström, Zetterström, 1991.
  4. Denis Vogel. Massey products in the Galois cohomology of number fields. — . — Шаблон:URN.
  5. Masanori Morishita. Analogies between Knots and Primes, 3-Manifolds and Number Rings. — . — arXiv:0904.3399.
  6. William Thurston. The Geometry and Topology of Three-Manifolds. — 2002. — 1 березня. — С. Ch 7. Computation of volume p. 165.
  7. ICM 2006
  8. Lakshminarayan, 2007.
  9. Blog entry by Arul Lakshminarayan
  10. Mao, Sun, Seeman, 1997, с. 137–138.
  11. Цю роботу опубліковано в журналі Science 2004, 304, 1308—1312. Abstract
  12. Kraemer, 2006, с. 315–318.
  13. Moskowitz, 2009.
  14. Tanaka, 2010, с. 062701.

Література
  • Clara Moskowitz. Strange Physical Theory Proved After Nearly 40 Years // Live Science. — 2009. — Вип. December 16.
  • K. Tanaka. Observation of a Large Reaction Cross Section in the Drip-Line Nucleus 22C // Physical Review Letters. — 2010. — Т. 104, вип. 6. — DOI:10.1103/PhysRevLett.104.062701.
  • T. Kraemer, M. Mark, P. Waldburger, J. G. Danzl, C. Chin, B. Engeser, A. D. Lange, K. Pilch, A. Jaakkola, H.-C. Nägerl and R. Grimm. Evidence for Efimov quantum states in an ultracold gas of caesium atoms // Nature. — 2006. — Т. 440, вип. 7082. — arXiv:cond-mat/0512394. — Bibcode: 2006Natur.440..315K. — DOI:10.1038/nature04626. — PubMed.
  • C. Mao, W. Sun, N. C. Seeman. Assembly of Borromean rings from DNA // Nature. — 1997. — Т. 386. — DOI:10.1038/386137b0. — PubMed.
  • Arul Lakshminarayan. Borromean Triangles and Prime Knots in an Ancient Temple. — Indian Academy of Sciences, 2007. — Вип. May.
  • P. R. Cromwell, E. Beltrami and M. Rampichini, «The Borromean Rings», Mathematical Intelligencer Vol. 20 no. 1 (1998) 53-62.
  • Michael H. Freedman, Richard Skora. Strange Actions of Groups on Spheres // Journal of Differential Geometry. — 1987. — Т. 25. — С. 75–98.
  • Bernt Lindström, Hans-Olov Zetterström. Borromean Circles are Impossible // American Mathematical Monthly. — 1991. — Т. 98, вип. 4. — С. 340–341. — DOI:10.2307/2323803. — JSTOR 2323803. Стаття пояснює, чому кільця Борромео не могут быть абсолютно круглыми
  • R. Brown, J. Robinson. Borromean circles. Letter // American Mathematical Monthly. — 1992. — Вип. 4 (April). — С. 376–377.. Стаття показує, що існують квадрати Борромео, і ці квадрати, а також іннші форми цієї структури втілив у скульптурі Джон Робінсон.
  • W. W. Chernoff. (English summary) 15th British Combinatorial Conference (Stirling, 1995). // Discrete Math.. — 1997. — Т. 167/168. — С. 197–204. Стаття розглядає й інші багатокутники.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.