Сума за клікою

Сума за клікою — теоретико-графова операція, що забезпечує комбінацію двох графів склеюванням їх за клікою, подібно до зв'язної суми в топології. Якщо два графи і містять кліки однакового розміру, сума за клікою утворюється з незв'язаного об'єднання графів ототожненням пар вершин із клік так, щоб утворити одну кліку, з подальшим видаленням деяких ребер[1]. Сума за -клікою — це сума за клікою, яка містить не більше вершин. Можна утворити суму за кліками і суму за -кліками більше ніж двох графів повторенням операції суми.

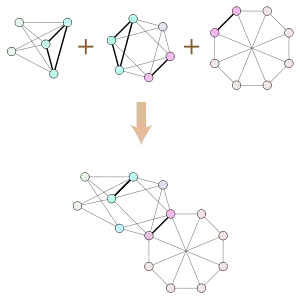
Сума за клікою двох планарних графів і графу Вагнера. В результаті отримуємо граф без K5.

Пов'язані концепції

Суми за клікою тісно пов'язані з деревною шириною — якщо деревна ширина двох графів не перевершує , то сума за -клікою буде мати таку саму властивість. Будь-яке дерево є сумою за 1-кліками його ребер. Будь-який паралельно-послідовний граф, або, узагальнено, будь-який граф з деревною шириною, що не перевищує двох, можна побудувати як суму за 2-кліками трикутників. Той самий результат узагальнюється для великих  — будь-який граф, деревна ширина якого не перевершує , можна побудувати як суму за кліками графів з не більше ніж вершинами, і в цьому випадку використовуються суми за -кліками[2].

Існує також близький зв'язок між сумами за кліками і зв'язністю графу — якщо граф не -зв'язний вершинно (так що існує множина з вершин, видалення яких призводить до втрати зв'язності), то граф можна подати у вигляді суми за -кліками дрібніших графів. Наприклад, SPQR-дерево двозв'язного графу є поданням графу як суми за 2-кліками його тризв'язних компонент.

Застосування в структурній теорії графів
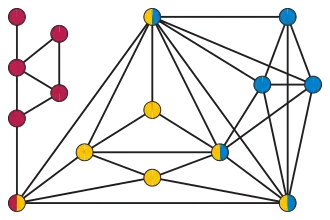
Стиснутий граф як сума за кліками найбільшого планарного графу (жовтий) і двох хордальных графів (червоний і блакитний)

Суми за кліками важливі в структурній теорії графів, де вони використовуються для опису деяких родин графів як графів, утворених сумою за кліками графів меншого розміру. Першим результатом такого типу[3] була теорема Вагнера[4], який довів, що графи, які не містять мінорами повних графів з п'ятьма вершинами, є сумою за 3-кліками планарних графів з графом Вагнера. За допомогою цієї структурної теореми можна показати, що проблема чотирьох фарб еквівалентна випадку гіпотези Хадвігера. Хордальні графи — це точно графи, які можна утворити як суми клік за кліками без видалення ребер, а стиснуті графи — це графи, які можна утворити як суми без видалення ребер за кліками клік і найбільших планарних графів[5]. Графи, в яких будь-який породжений цикл довжини чотири або більше утворює мінімальний розділювальний підграф (після його видалення граф розпадається на дві або більше незв'язних компонент, і жодна підмножина циклу не має такої ж властивості), є точно сумами за кліками клік і максимальних планарних графів, знову без видалення ребер[6]. Джонсон і Маккі[7] використовували суми за кліками хордальних графів і паралельно-послідовних графів для опису частково визначених[8] матриць, які мають додатно означене довизначення.

Можна отримати розклад за сумами за кліками для будь-якого сімейства графів, замкнутого відносно операції мінора — графи в будь-якому мінорно-замкнутому сімействі можна утворити з сум за кліками графів, які «майже вкладені» на поверхні скінченного роду, що означає, що вкладення дозволено щоб уникнути невеликого числа дахів (вершин, які можна з'єднати з довільним число інших вершин) і лійок (графи з малою шляховою шириною, які замінюють грані при вкладанні на поверхню)[9]. Ці описи використовувалися як важливий засіб під час побудови апроксимаційних алгоритмів і субекспоненціальних за часом точних алгоритмів для NP-повних задач оптимізації на мінорно-замкнутих сімействах графів[10][11][12].

Узагальнення

Теорію сум за кліками можна узагальнити від графів до матроїдів. Теорема розкладання Сеймура описує регулярні матроїди (матроїди, які представляють цілком унімодулярні матриці) як 3-суми графічних матроїдів (матроїди, що представляють головні дерева), кографічні матроїди і деякі 10-елементні матроїди[13].

Примітки
  1. Тут є деяка невизначеність. У книзі Окслі (Oxley, 1992) йдеться, що слід видалити всі ребра клік. Д. Епштейн (у поясненнях до англійського варіанта статті) стверджує, що в деяких застосуваннях можна вибирати, які ребра видаляти, а які можна залишити, а в деяких застосуваннях можна видаляти взагалі.
  2. Lovász, 2006.
  3. Як зазначили Криж і Томас (Kříž, Thomas, 1990), які перелічили деякі додаткові описи сімейств графів, що спираються на суми за кліками.
  4. Wagner, 1937.
  5. Seymour, Weaver, 1984.
  6. Diestel, 1987.
  7. Johnson, McKee, 1996.
  8. Частково визначена матриця — це матриця, не всі клітинки якої заповнено. Такі матриці використовують у теорії експертних оцінок, в рекомендаційних системах.
  9. Robertson, Seymour, 2003.
  10. Demaine (1), 2004.
  11. Demaine (2), 2005.
  12. Demaine (3), 2005.
  13. Seymour, 1980.

Література
  • Erik D. Demaine, Fedor V. Fomin, MohammedTaghi Hajiaghayi, Dimitrios Thilikos. Subexponential parameterized algorithms on bounded-genus graphs and H-minor-free graphs // Journal of the ACM. — 2005. — Т. 52, вип. 6 (21 січня). — С. 866—893. — DOI:10.1145/1101821.1101823.
  • Erik D. Demaine, MohammedTaghi Hajiaghayi, Naomi Nishimura, Prabhakar Ragde, Dimitrios Thilikos. Approximation algorithms for classes of graphs excluding single-crossing graphs as minors // Journal of Computing and Systems Sciences. — 2004. — Т. 69, вип. 2 (21 січня). — С. 166—195. — DOI:10.1016/j.jcss.2003.12.001.
  • Erik D. Demaine, Mohammed Taghi Hajiaghayi, Ken-ichi Kawarabayashi. Proc. 46th IEEE Symp. Foundations of Computer Science (PDF). — 2005. — 21 січня. — С. 637—646. — DOI:10.1109/SFCS.2005.14.
  • Reinhard Diestel. A separation property of planar triangulations // Journal of Graph Theory. — 1987. — Т. 11, вип. 1 (21 січня). — С. 43—52. — DOI:10.1002/jgt.3190110108.
  • Igor Kříž, Robin Thomas. Clique-sums, tree-decompositions and compactness // Discrete Mathematics. — 1990. — Т. 81, вип. 2 (21 січня). — С. 177–185. — DOI:10.1016/0012-365X(90)90150-G.
  • Charles R. Johnson, Terry A. McKee. Structural conditions for cycle completable graphs // Discrete Mathematics. — 1996. — Т. 159, вип. 1–3 (21 січня). — С. 155–160. — DOI:10.1016/0012-365X(95)00107-8.
  • László Lovász. Graph minor theory // Bulletin of the American Mathematical Society. — 2006. — Т. 43, вип. 1 (21 січня). — С. 75–86. — DOI:10.1090/S0273-0979-05-01088-8.
  • N. Robertson, P. D. Seymour. Graph minors XVI. Excluding a non-planar graph // Journal of Combinatorial Theory, Series B. — 2003. — Т. 89, вип. 1 (21 січня). — С. 43–76. — DOI:10.1016/S0095-8956(03)00042-X.
  • P. D. Seymour. Decomposition of regular matroids // Journal of Combinatorial Theory, Series B. — 1980. — Т. 28, вип. 3 (21 січня). — С. 305–359. — DOI:10.1016/0095-8956(80)90075-1.
  • P. D. Seymour, R. W. Weaver. A generalization of chordal graphs // Journal of Graph Theory. — 1984. — Т. 8, вип. 2 (21 січня). — С. 241–251. — DOI:10.1002/jgt.3190080206.
  • Klaus Wagner. Über eine Eigenschaft der ebenen Komplexe // Mathematische Annalen. — 1937. — Т. 114 (21 січня). — С. 570–590. — DOI:10.1007/BF01594196.
  • James G. Oxley. Matroid Theory. — New York, Tokyo : Oxford University Press, 1992. — С. 420. — ISBN 0-19-853563-5.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.