Сферична астрономія

У той час, як астрометрія на практиці реалізує вимірювання положень і відносних рухів астрономічних об'єктів, сферична астрономія як більш теоретична дисципліна, тісно пов'язана з математикою, займається питаннями встановлення небесних систем координат і систем відліку часу, а також переходів між ними. Фактично основним завданням сферичної астрономії є редукція спостережень, тобто вирахування координат і швидкостей небесних тіл в певній системі координат на заданий момент часу, виходячи з їхніх спостережень[1].

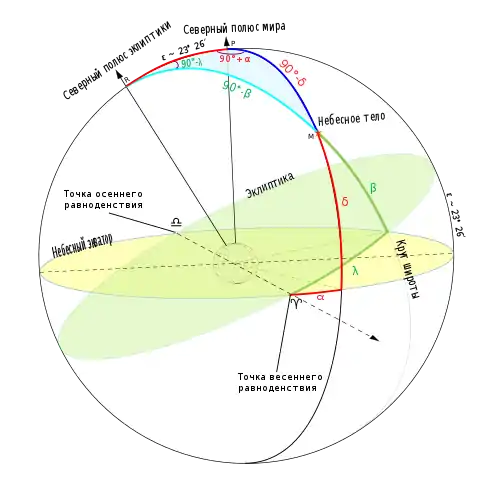
Основне поняття сферичної астрономії — небесна сфера, тобто уявна сфера довільного радіусу з центром в спостерігачі, на яку проектуються видимі положення астрономічних об'єктів і на якій вводяться небесні системи координат, найуживаніші з яких: горизонтальна, дві екваторіальні, екліптична і галактична. Переходи між ними здійснюються за формулами сферичної тригонометрії[1].

Основні елементи сферичної астрономії — це системи координат і час. Для вказівки положення небесних тіл використовується екваторіальна система координат, заснована на проекції екватора Землі на небесну сферу. Положення об'єкта визначається його прямим сходженням (α) і відміною (δ). На основі цих даних, широти і місцевого часу можна визначити положення об'єкта в горизонтальній системі координат, а саме його висоту і азимут[1].

Сферична астрономія є базисом для астрономії в цілому і має численні застосування. У фундаментальній астрономії в результаті обробки скорочених астрометричних спостережень визначаються параметри небесних систем координат і шкал часу, а також уточнюються параметри редукції і складаються системи астрономічних постійних. У прикладної астрономії сферична астрономія використовується в процесі вирішення завдань навігації, тобто визначення координат спостерігача, як на Землі, так і в космосі[1].

Астрономія зародилася з потреби у визначенні моментів певних подій, як господарського так і релігійного значення. Встановлення календаря потрібно для землеробства, і тому вже стародавні мешканці Месопотамії і Єгипту досить точно визначили тривалість року, а також по довгих ланцюжках сонячних і місячних затемнень навчилися їх передбачати. 60-річної системі числення стародавніх вавилонян досі використовується за рахунку часу[2].

Подальший прогрес пов'язаний з розквітом філософії і математики в Стародавній Греції. Перший давньогрецький астроном Фалес (кінець VII-перша половина VI століття до н. Е.) — Один з «семи мудреців», за переказами, встановив час рівнодення і сонцестояння, визначив тривалість року в 365 діб і зрозумів те, що Місяць світить не сам, і так далі. У той же час Землю він вважав плоским диском, а причин затемнень не розумів[2].

Розробка перших строгих математичних теорій астрономії належить Евдоксу Книдському (близько 400—355 роки до н. Е.). Виходячи зі сфери і кола як ідеальних фігур, він придумав систему розкладання видимого руху Сонця і планет на рівномірні обертання сфер, що захоплюють за собою інші сфери, до останньої з яких на екваторі прикріплено небесне тіло. У його моделі було 27 таких сфер, у Каліппа — 34, а Аристотель (384—322 роки до н. е.), завдяки авторитету якого ця модель стала домінуючою, розглядав уже 56 сфер[2].

Астрономи-спостерігачі Арістілл і Тімохаріс (III століття до н. Е.) Були піонерами визначень положень зірок і склали перший зоряний каталог в екваторіальній системі, знайшовши прямі сходження і відміни зірок. Ератосфен з Кірени (276—194 роки до н. е.) визначив з точністю до 50 км радіус Землі і з точністю до 8 секунд дуги нахил екліптики до екватора[2].

Геліоцентрична теорія Коперника, опублікована в 1543 році, була наступним великим кроком, значення якого було зрозуміле лише згодом, після робіт Тихо Браге (1546—1601), який досяг найкращої відомої точності спостережень зірок і планет неозброєним оком і склав новий каталог 777 зірок з точністю положень в половину хвилини дуги. Його спостереження Марса дозволили Кеплеру вивести закони руху планет, що остаточно підтвердило пріоритет геліоцентричної системи[2].

До кінця XVIII століття механічні годинники випускалися десятками тисяч штук, їх механізми швидко вдосконалюються, а точність підвищується. Глобалізація торгівлі та переміщень людей зажадала введення єдиного часу, і в 1884 році на міжнародній конференції у Вашингтоні було прийнято поясний час, початком відліку якого став Гринвіцький час — середній сонячний час на обраному нульовому меридіані, меридіані Гринвіча. Там же визначили лінію зміни дат[2].

Винахід телескопа в XVII столітті Галілеєм і вдосконалення його Ньютоном призвело до швидкого прогресу точності астрономічних спостережень. У 1725 році англійський королівський астроном Джеймс Брадлей вивів зі спостережень аберацію світла, яка виявляється у вигляді періодичної зміни видимих ​​положень зірок через зміну напрямку і величини швидкості руху Землі відносно них. У 1837 році Фрідріх Бессель вперше зумів виміряти також річний паралакс зірки — відносне зміщення зірки 61 Лебедя щодо найближчих до неї через зміну положення спостерігача разом із Землею в просторі[2].

Спостереження Місяця і Сонця, в тому числі стародавні, при порівнянні з точними теоріями руху Сонячної системи кінця XIX—початку XX століття, розробленими Ньюкомбом, Брауном і де Сіттера, привели до виявлення вікового уповільнення обертання Землі. Теорія руху Сонця Ньюкомба була настільки точною, що стала основою створення першої динамічної шкали часу — шкали ефемеридного часу, і визначення ефемеридної секунди. Тільки до середини XX століття точність годинників — атомних стандартів частоти — стала кращою, ніж для ефемеридного часу, і перехід до атомної шкали дозволив безпосередньо виміряти нерівномірність обертання Землі[2].

Новий розвиток техніки спостережень в кінці XX століття — лазерна далекометрія і інші методи — дозволили ще підвищити точність вимірів до міліметрової точності, змушуючи враховувати вже і релятивістські ефекти відхилення і запізнювання електромагнітних сигналів в гравітаційних полях, що було офіційно закріплено рішеннями Міжнародного астрономічного союзу в 2000 році.

Використання високоточної техніки дозволило виміряти гравітаційне поле Землі, виміряти ефект впливу гравітаційного поля на швидкість ходу годинника і впровадити в практику глобальні супутникові навігаційні системи GPS (Global Positioning System) і ГЛОНАСС (Глобальна Навігаційна Супутникова Система). Нові опорні каталоги, щодо яких визначаються небесні координати, досягли точності в 0,1 мілісекунди дуги в радіо і одиниць мілісекунд в оптичному діапазоні[3].

• Сферична астрономія: навч. посіб. / Ф. Д. Заблоцький, С. Г. Савчук, Ю. О. Лук‘янченко та ін. — Львів: Львівська політехніка, 2019. — 152 с. — ISBN 966-941-353-6.
• Robin M. Green, Spherical Astronomy, 1985, Cambridge University Press, ISBN 0-521-31779-7
• William M. Smart, edited by Robin M. Green, Textbook on Spherical Astronomy, 1977, Cambridge University Press, ISBN 0-521-29180-1.
• Жаров В. Е. Сферическая астрономия. — М., 2006. — 480 с. — (Монографии и учебники). — 500 екз. — ISBN 5-85099-168-9.

• Сферическая астрономия. БСЭ, 1969—1978. Яндекс.Словари. Архів оригіналу за 27 лютого 2013. Процитовано 27 лютого 2013.