Тангенціальний трикутник
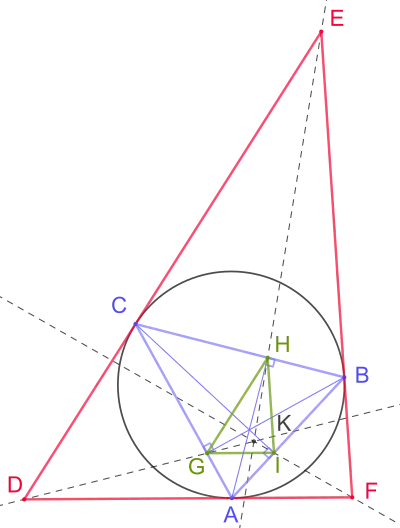
Якщо навколо даного гострокутного трикутника описати коло і в трьох вершинах трикутника провести прямі, дотичні до кола, то перетин цих прямих утворює так званий тангенціальний трикутник по відношенню до даного трикутника . Трикутник по відношенню до трикутника називають тангенціальним трикутником, бо його сторони , і є дотичними до кола, описаного навколо даного трикутника відповідно в вершинах , і .
Зауваження
Тангенціальний по латині означає дотичний, хоча термін дотичний трикутник може мати і кілька більш загальний сенс, як трикутник, на сторонах якого лежать вершини даного трикутника .
Координати вершин
Трикутні координати вершин тангенціального трикутника
Властивості
- Сторони тангенціального трикутника антипаралельні відповідним протилежним сторонам даного трикутника (по властивості антипаралельності дотичних до кола).
- Сторони тангенціального трикутника паралельні відповідним сторонам Ортотрикутника.
- Вписане в тангенціальний трикутник коло є описаним колом по відношенню до даного трикутника .
- Центр вписаного в тангенціальний трикутник кола збігається з центром кола, описаного близько даного трикутника .
- Зв'язок між кутами тангенціального трикутника і даного трикутника ΔABC
- Центр вписаного в тангенціальний трикутник кола збігається з центром кола, описаного близько даного трикутника .
- Для даного трикутника його тангенціальний трикутник і Ортотрикутник подібні.
- Площа даного трикутника дорівнює середньому геометричному між площами тангенціального трикутника і Ортотрикутника.
- Площа тангенціального трикутника дорівнює [1]:
де - площа трикутника ; - його відповідні сторони.
Або[2]
- Сторони тангенціального трикутника дорівнюють[2]
Властивості подібності родинних трикутників
- Вихідний трикутник по відношенню до Ортотрикутника є трикутником трьох зовнішніх бісектрис.
- Ортотрикутник і тангенціальний трикутник подібні (Зетель, 1962, наслідок 1, § 66).
- Ортотрикутник Ортотрикутника і вихідний трикутник подібні.
- Трикутник трьох зовнішніх бісектрис трикутника трьох зовнішніх бісектрис і вихідний трикутник подібні.
- Ортотрикутник трикутника Жергонна і вихідний трикутник подібні.
- Вище зазначені властивості подібності родинних трикутників є наслідком нижче перерахованих властивостей паралельності (антипаралельності) сторін родинних трикутників.
Властивості паралельності (антипаралельності) сторін родинних трикутників
- Сторони даного гострокутного трикутника антипаралельні відповідним сторонам Ортотрикутник, проти яких вони лежать.
- Сторони тангенціального трикутника антипаралельні відповідним протилежним сторонам даного трикутника (по властивості антипаралельності дотичних до кола).
- Сторони тангенціального трикутника паралельні відповідним сторонам Ортотрикутник.
- Нехай, точки дотику вписаного в даний трикутник кола з'єднані відрізками, тоді вийде трикутник Жергонна, і в отриманому трикутнику проведено висоти. В цьому випадку прямі, що з'єднують підстави цих висот, паралельні сторонам вихідного трикутника. Отже Ортотрикутник трикутника Жергонна і вихідний трикутник подібні.
Чудові точки
Наступна таблиця дає відповідність чудових точок тангенціального трикутника з центрами вихідного трикутника. Xn означає індекс чудової точки в списку Кімберлінга [3].
| Xn | Центр тангенціального трикутника | Xn | Центр вихідного трикутника |
|---|---|---|---|
| X2 | центроїд трикутника | X154 | X3 чева-сполучена точка до X6 |
| X3 | центр описаного кола | X26 | центр описаного кола тангенціального трикутника |
| X4 | Ортоцентр | X155 | власний центр Ортотрикутник |
| X5 | центр дев'яти точок | X156 | X5 тангенціального трикутника |
| X6 | точка перетину симедіан | X157 | X6 тангенціального трикутника |
| X30 | нескінченна точка прямої Ейлера | X1154 | ізогональне сполучення точки X1141 |
| X523 | ізогональне сполучення точки X110 | X1510 | крос-різниця точок Наполеона |
Див. також
Примітки
- Формулу можна вивести з попередньої властивості і площі Ортотрикутник
- Шаблон:MathWorld3
- Енциклопедія центрів трикутника