Танграм

Танграм (кит.: 七巧板; піньїнь: qī qiǎo bǎn; літ.: 'сім дощечок майстерності') — це головоломка, яка складається з семи гральних кісток — пласких геометричних фігур, які називають танами, що складаються у різні форми. Завдання головоломки — створити задану форму (на підставі лише обрису силуету) з використанням всіх семи танів, які заборонено накладати один на один. Це одна з найбільш популярних головоломок такого типу у світі.[1][2] Китайський психолог назвав танграм «найдавнішим психологічним тестом світу», хоча і створеним для розваги, а не для аналізу.[3]

Які і більшість сучасних наборів, цей дерев'яний танграм зберігається у квадратній конфігурації.

Походження назви

Західна назва головоломки, танграм, швидше за все створена поєднанням двох слів, китайського слова танг, посилання на китайську династію Тан, та грецького слова грамма, синоніму кореня граф (напр., «графік»).[4]

Легенда

Згідно з легендою, одного разу чернець завдав своєму учню задачу здійснити подорож для того, щоб намалювати суть різноманітної краси світу тільки на одній керамічній дощечці. На жаль, дощечка розбилася на сім шматків і учень ніяк не міг її знову зібрати у квадратну форму.

Він намагався це зробити багато днів поспіль, намалював численні зразки та зображення. Наприкінці учень зрозумів: немає сенсу подорожувати в світ, бо легко можна знайти всю красу і різноманітність світу у семи шматках розбитої дощечки.

Історія

Танграм є дуже старою китайською грою на гральних кістках, яка за однією з версій ймовірно була винайдена між VIII та IV століттям до н. е., а за іншою — значно пізніше — під час правління династії Сун[3]. Після того, як в Китаї почали друкувати книжки з танграмами, гра була завезена до Європи та Америки торговими кораблями на початку XIX століття, де стала дуже популярною на деякий час, та вдруге — під час Першої світової війни.

Прибуття на Захід (1815-1820-ті роки)
Французька карикатура 1818 року, коли захоплення танграмом було на піку. Напис: " 'Бережіть себе, бо Ви не сталеві. Вогонь майже згас, а надворі зима.' 'Я був зайнятий всю ніч. Дозвольте я Вам поясню. Ви граєте в цю гру, яка, подейкують, походить з Китаю. А я Вам кажу, зараз Парижу потрібно вітати те, що приходить здалеку.' "

В Америку танграм вперше було принесено в 1815 році капітаном М.Дональдсоном, якому в Кантоні подарували дві книги танграм авторства Sang-Hsia-koi.[5] Перша книжка з танграмами в Америці була надрукована на підставі цих двох книжок.

Головоломка набула популярності завдяки Восьмій книзі Тана, вигаданій історії танграму, яка стверджувала, що гра була вигадана 4 000 років до того богом Таном. Книга включала 700 фігур, деякі з яких можливо вирішити.[6]

Після цього, головоломка досягла Англії, де стала дуже популярною, і швидко поширилась на інші європейські країни.[5] Це відбулось переважно завдяки двом британським книгам з танграмами: Модна китайська головоломка та книзі-доповненню з розв’язками, Ключ.[7] Невдовзі набори танграм почали в значних кількості експортуватись з Китаю, де їх робили з різних матеріалів — скла, дерева, панцирів черепах.[8]

Багато цих незвичних та дорогих наборів попали до Данії і данський інтерес до танграмів вистрелив близько 1818 року, коли було надруковано дві книги з цими головоломками.[9] Перша з них — Мандарини, написана студентом Копенгагенського університету, нехудожній твір про історію та популярність танграмів. Друга — Нова китайська головоломка, що складалася з 339 головоломок, скопійованих з Восьмої книги Тана, і однієї оригінальної.[9]

Фактором, який сприяв популярності гри у Європі, було те, що хоча римо-католицька церква і забороняла багато видів розваг у неділю і святі дні, вона не заперечувала проти таких головоломок, як танграм.[10]

Друга хвиля популярності (Німеччина та США, 1891–1920 рр.)

Німецькій публіці танграми були вперше презентовані промисловцем Ф. А. Ріхтером, засновником фабрики Anker, у 1891 році.[11] Як і інші головоломки фабрики (будівельні набори Anker), набори для танграму виготовлялись з каміння або штучної кераміки,[12] та продавались під назвою «головоломка Anker».[11]

На міжнародному рівні, Перша світова війна сприяла значному відновленню інтересу до цієї гри, в яку грали і вдома, і в окопах, усі сторони конфлікту. Протягом цього часу, гра деколи була відома під назвою «Сфінкс», як альтернатива до наборів «головоломок Anker».[13][14]

Третя хвиля популярності (Німеччина/Голландія, з 1976 р.)

З середини 1970-х років почалося відновлення популярності гри, коли видавництво DuMont почало випускати кишенькові книжки з головоломками двома мовами — німецькою та голландською, в яких представлено близько 1600 фігур. Подібні ігри популярні і зараз, їх виготовляють і продають по всьому світі. Існують танграми українського виробництва[джерело?].

Елементи (тани) головоломки

Якщо обрати одиницю вимірювання таким чином, що сім елементів можуть бути зібрані в квадрат зі стороною одиниця та площею — квадратна одиниця, то сім елементів будуть такими:

  • 2 великих прямокутні трикутники (гіпотенуза , сторони , площа )
  • 1 середній прямокутний трикутник (гіпотенуза , сторони , площа )
  • 2 малих прямокутний трикутники (гіпотенуза , сторони , площа )
  • 1 квадрат (сторони , площа )
  • 1 паралелограм (сторони: та , площа )

Серед цих семи танів паралелограм є особливим, оскільки він не має осьової симетрії, а лише обертальну симетрію, і тому його дзеркальне зображення може бути отримано лише перевертанням цього елементу. Тому це єдиний тан, який при складанні певних фігур слід перевертати.

Кількість конфігурацій
13 випуклих форм з набору танграм

Лише з текстів 19-го сторіччя було створено більше 6500 задач для танграму і поточне число весь час зростає.[15] Однак, відомо, що кількість фігур є кінцевою.

Fu Traing Wang та Chuan-Chin Hsiung в 1942 році довели, що існує лише 13 опуклих конфігурацій танграму (тобто таких, в яких відрізок, проведений між двома будь-якими точками меж (ободу) конфігурації повністю проходить через тіло конфігурації).[16][17]

Парадокси

Парадокс танграму — це омана розсічення: дві фігури складаються з двох однакових наборів елементів, одна з яких здається точною підмножиною іншої.[18] Одним з відомих парадоксів є «два монахи», створення якого приписується Генрі Дудені та який складається з двох схожих фігур, одна з яких має ногу, а друга — ні.[19] Насправді нестача ноги компенсується у другій фігурі дещо більшим тілом.

Інший парадокс був запропонований Семом Лойдом у Восьмій книзі Тана:

Сьома та восьма фігури є містичними квадратами, побудованими з семи елементів: одна квадрат, а друга з відрізаним кутом, і при цьому задіяно всі сім елементів.[20]

Галерея парадоксів
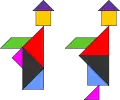  • Два монахи - схожі фігури, один без ноги.
  • Магічна чаша для гральних кубиків із Восьмої книги Тана (1903). Кожна з цих чаш створена з одних і тих же семи елементів, однак перша чаша - повна, а дві інші містять пустоти різної форми (зверніть увагу, що чаша зліва коротша за дві інші; та, що всередині, трохи ширша за ту, що справа).[21]
  • Обрізаний квадрат.

Варіанти

Існує досить багато варіантів танграму. Деякі з них:

  • трикутний танграм — прямокутник, розрізаний на три трикутники різного розміру. З трьох елементів можливо зібрати лише 16 фігур
  • Т-головоломка — літера «T» з шириною а малюється на папері чи тонкій дощечці та розрізується: першим розрізом на три частини, другий розріз здійснюється паралельно першому на відстані а, що утворює всього 4 елементи.
  • Остомахіон (Loculus Archimedicus) — квадрат, розрізаний на 14 елементів. Задача знайдена у рукописі з такою назвою; приписується Архімеду (знайдено копії арабською мовою та неповну — грецькою). Вважається, що гра давніша за рукопис, з елементів складали багато фігур — тварин і т. д. У рукописі Архімед розмірковував, скількома способами можливо скласти квадрат. У сучасні часи шляхом перебору було отримано результат — 17 152 способи.
  • Яйце Колумба (головоломка) — головоломка, яка складається з 9 елементів, отриманих розрізанням форми, схожої на яйце, прямими лініями.

Галерея варіантів
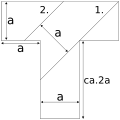  • Т-головоломка (показано лінії побудови)
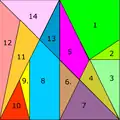  • Остомахіон (один із варіантів складення у квадрат)
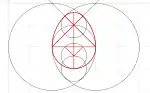  • Яйце Колумба (показано лінії побудови)

Примітки
  1. Slocum, Jerry (2001). The Tao of Tangram. Barnes & Noble. с. 9. ISBN 978-1-4351-0156-2.
  2. Forbrush, William Byron (1914). Manual of Play. Jacobs. с. 315. Процитовано 10/13/10.
  3. Jiannong Shi (2 лютого 2004). У Robert J. Sternberg. International Handbook of Intelligence. Cambridge University Press. с. 330–331. ISBN 978-0-521-00402-2.
  4. The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. Mathematical Association of America. 1994. с. 218. ISBN 978-0-88385-511-9.
  5. Slocum, Jerry (2003). The Tangram Book. Sterling. с. 30. ISBN 9781402704130.
  6. Costello, Matthew J. (1996). The Greatest Puzzles of All Time. New York: Dover Publications. ISBN 0-486-29225-8.
  7. Slocum, Jerry (2003). The Tangram Book. Sterling. с. 31. ISBN 9781402704130.
  8. Slocum, Jerry (2003). The Tangram Book. Sterling. с. 49. ISBN 9781402704130.
  9. Slocum, Jerry (2003). The Tangram Book. Sterling. с. 99–100. ISBN 9781402704130.
  10. Slocum, Jerry (2003). The Tangram Book. Sterling. с. 51. ISBN 9781402704130.
  11. http://www.archimedes-lab.org/tangramagicus/pagetang1.html
  12. Treasury Decisions Under customs and other laws, Volume 25. United States Department Of The Treasury. 1890–1926. с. 1421. Процитовано 9/16/10.
  13. Wyatt (26 квітня 2006). Tangram – The Chinese Puzzle. BBC. Процитовано 3 жовтня 2010.
  14. Braman, Arlette (2002). Kids Around The World Play!. John Wiley and Sons. с. 10. ISBN 978-0-471-40984-7. Процитовано 9/5/2010.
  15. Slocum, Jerry (2001). The Tao of Tangram. Barnes & Noble. с. 37. ISBN 978-1-4351-0156-2.
  16. Fu Traing Wang; Chuan-Chih Hsiung (November 1942). A Theorem on the Tangram. The American Mathematical Monthly 49 (9): 596–599. JSTOR 2303340. doi:10.2307/2303340.
  17. Read, Ronald C. (1965). Tangrams : 330 Puzzles. New York: Dover Publications. с. 53. ISBN 0-486-21483-4.
  18. Парадокс танграм на MathWorld від Маргерити Баріле
  19. Dudeney, H. (1958). Amusements in Mathematics. New York: Dover Publications.
  20. Loyd, Sam (1968). The eighth book of Tan – 700 Tangrams by Sam Loyd with an introduction and solutions by Peter Van Note. New York: Dover Publications. с. 25.
  21. http://www.futilitycloset.com/2011/04/02/the-magic-dice-cup/

Джерела
  • Anno, Mitsumasa. Anno's Math Games (three volumes). New York: Philomel Books, 1987. ISBN 0-399-21151-9 (v. 1), ISBN 0-698-11672-0 (v. 2), ISBN 0-399-22274-X (v. 3).
  • Botermans, Jack, et al. The World of Games: Their Origins and History, How to Play Them, and How to Make Them (translation of Wereld vol spelletjes). New York: Facts on File, 1989. ISBN 0-8160-2184-8.
  • Dudeney, H. E. Amusements in Mathematics. New York: Dover Publications, 1958.
  • Гарднер, Мартін. «Mathematical Games—on the Fanciful History and the Creative Challenges of the Puzzle Game of Tangrams», Scientific American Aug. 1974, p. 98-103.
  • Гарднер, Мартін. «More on Tangrams», Scientific American Sep. 1974, p. 187-191.
  • Гарднер, Мартін. The 2nd Scientific American Book of Mathematical Puzzles and Diversions. New York: Simon & Schuster, 1961. ISBN 0-671-24559-7.
  • Loyd, Sam. Sam Loyd's Book of Tangram Puzzles (The 8th Book of Tan Part I). Mineola, New York: Dover Publications, 1968.
  • Slocum, Jerry, et al. Puzzles of Old and New: How to Make and Solve Them. De Meern, Netherlands: Plenary Publications International (Europe); Amsterdam, Netherlands: ADM International; Seattle: Distributed by University of Washington Press, 1986. ISBN 0-295-96350-6.
  • Slocum, Jerry, et al. The Tangram Book: The Story of the Chinese Puzzle with Over 2000 Puzzles to Solve. New York: Sterling Publishing Company, 2003. ISBN 9781402704130.
  • Erwin Glonnegger: Das Spiele-Buch: Brett- und Legespiele aus aller Welt; Herkunft, Regeln und Geschichte. Uehlfeld: Drei-Magier-Verlag, 1999. ISBN 3-9806792-0-9
  • Daniel Picon: Tangram. Spielen — denken — lernen. Mehr als 1000 Aufgaben und Lösungen; 2004; ISBN 3-89717-277-1
  • Joost Elffers: Tangram. Das alte chinesische Formenspiel — Het oude Chinese vormenspel. DuMont Buchverlag Köln. 1978; ISBN 3-7701-0899-X

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.