Теорема котангенсів

У тригонометрії, теорема котангенсів пов'язує радіус кола, вписаного у трикутник, з довжиною його сторін. Теорему котангенсів зручно використовувати при розв'язуванні трикутника за трьома сторонами.

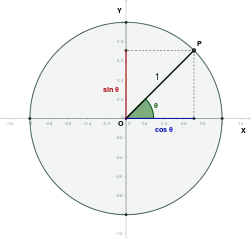
Тригонометрія
Обрис Історія Застосування Функції (обернені) Узагальнена тригонометрія
Посилання
Тотожності Точні сталі Таблиці Одиничне коло
Закони і теореми
Синуси Косинуси Тангенси Котангенси Теорема Піфагора
Обчислення
Тригонометричні підстановки Інтеграли (обернені функції) Похідні

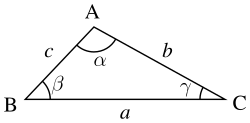
Трикутник загального виду

Нехай ${\displaystyle a}$, ${\displaystyle b}$ і ${\displaystyle c}$ — довжини трьох сторін трикутника, ${\displaystyle \alpha ,\beta }$ і ${\displaystyle \gamma }$ — кути, що лежать навпроти, відповідно, сторін ${\displaystyle a}$, ${\displaystyle b}$ і ${\displaystyle c}$ відповідно.

Теорема котангенсів стверджує, що якщо

${\displaystyle r={\sqrt {{\frac {1}{p}}(p-a)(p-b)(p-c)}}}$ (радіус кола, вписаного у трикутник) і

${\displaystyle p={\frac {a+b+c}{2}}}$ (півпериметр трикутника),

то справедливі наступні формули:[1]

${\displaystyle \operatorname {ctg} {\frac {A}{2}}={\frac {p-a}{r}},}$

${\displaystyle \operatorname {ctg} {\frac {B}{2}}={\frac {p-b}{r}},}$

${\displaystyle \operatorname {ctg} {\frac {C}{2}}={\frac {p-c}{r}},}$

звідки слідує, що

${\displaystyle {\frac {p-a}{\operatorname {ctg} {\tfrac {A}{2}}}}={\frac {p-b}{\operatorname {ctg} {\tfrac {B}{2}}}}={\frac {p-c}{\operatorname {ctg} {\tfrac {C}{2}}}}=r}$.

Словами теорему можна сформулювати так: котангенс половинного кута дорівнює відношенню півпериметра мінус довжина протилежної сторони вказаного кута до радіуса вписаного кола.

У сферичній тригонометрії існує схожа формула для половини кута, а також двоїста до неї формула половини сторони.