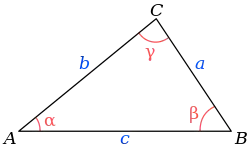Теорема синусів

Теорема синусів — наступне тригонометричне твердження про властивості кутів та сторін довільного трикутника: нехай a, b і c є сторонами трикутника, а A, B і C — кути протилежні вказаним сторонам, тоді

{\sin A \over a}={\sin B \over b}={\sin C \over c}

Ця формула корисна при обчисленні решти двох сторін трикутника, якщо відомі сторона та два прилеглі кути; типова проблема, що постає при тріангуляції. Також, якщо відомі дві сторони та один із кутів, що не утворюється цими сторонами, зазначена формула дає два можливих значення для внутрішнього кута. В цьому випадку, часто лишень одне значення задовольняє умові, що сума трьох кутів трикутника дорівнює 180°; інакше отримаємо два можливих розв'язки.

Обернене значення числа в теоремі синусів (тобто a/sin(A)) дорівнює діаметру D (або ж 2-ом радіусам) описаного навколо трикутника кола (єдине коло, що проходить через три точки A, B і C). Таким чином теорему можна переписати у розширеній формі

{a \over \sin A}={b \over \sin B}={c \over \sin C}=D=2R

Доведення

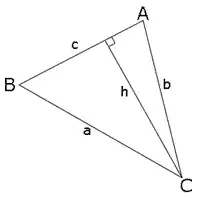
Нехай дано трикутник зі сторонами a, b, і c, з протилежними кутами A, B, і C. Опустимо перпендикуляр довжиною h з C на c.

Бачимо, що, за означенням:

\sin A={\frac {h}{b}}

та

\;\sin B={\frac {h}{a}}

Звідси:

h=b\,\sin A=a\,\sin B

також

{\frac {\sin A}{a}}={\frac {\sin B}{b}}

Повторимо операцію з кутом A і стороною a, і дістанемо:

{\frac {\sin B}{b}}={\frac {\sin C}{c}}

.∎

Доведення розширеної форми теореми синусів

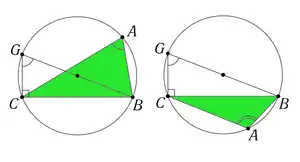
Достатньо довести, що

{\frac {a}{\sin \alpha }}=2R.

Проведемо діаметр $|BG|$ описаного кола. За властивістю кутів, уписаних у коло, кут $GCB$ прямий, а кут $CGB$ дорівнює або $\alpha$ , якщо точки $A$ і $G$ лежать по один бік від прямої $BC$ , або $\pi -\alpha$ в іншому разі. Оскільки $\sin(\pi -\alpha )=\sin \alpha$ , в обох випадках маємо

a=2R\sin \alpha

.

Повторивши ці міркування для двох інших сторін трикутника, маємо:

{\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}=2R.

∎

Доведення через формули знаходження площі трикутника

Візьмемо дві формули для знаходження площі трикутника $S={\frac {abc}{4R}}$ і $S={\frac {1}{2}}ab\sin \gamma .$

${\begin{cases}{\frac {abc}{4R}}={\frac {1}{2}}ab\sin \gamma \\{\frac {abc}{4R}}={\frac {1}{2}}ac\sin \beta \\{\frac {abc}{4R}}={\frac {1}{2}}bc\sin \alpha \end{cases}}\Leftrightarrow {\begin{cases}{\frac {c}{2R}}=\sin \gamma \\{\frac {b}{2R}}=\sin \beta \\{\frac {a}{2R}}=\sin \alpha \end{cases}}\Leftrightarrow {\begin{cases}2R={\frac {c}{\sin \gamma }}\\2R={\frac {b}{\sin \beta }}\\2R={\frac {a}{\sin \alpha }}\end{cases}}\Leftrightarrow 2R={\frac {a}{\sin \alpha }}={\frac {b}{\sin \beta }}={\frac {c}{\sin \gamma }}.$ ∎

Варіації та узагальнення

У трикутнику навпроти більшого кута лежить більша сторона, навпроти більшої сторони лежить більший кут.
У симплексі

V_{n}={\frac {n-1}{n}}\cdot {\frac {{V_{n-1}^{i}}{V_{n-1}^{j}}}{V_{n-2}^{i,j}}}\cdot \sin {A_{i,j}},

де $A_{i,j}$ — кут між гранями $V_{n-1}^{i}$ і $V_{n-1}^{j}$ ; $V_{n-2}^{i,j}$ — спільна грань $V_{n-1}^{i}$ і $V_{n-1}^{j}$ ; $V_{n}$ — об'єм симплекса.

Історія

У першій главі Альмагеста (бл. 140 року н. е.) теорему синусів використано, але явно не сформульовано[1].
Найдавніше з доведень, що дійшли до нас, теореми синусів на площині описано в книзі Насир ад-Діна ат-Тусі «Трактат про повний чотирибічник» написаній у XIII столітті[2].
Теорему синусів для сферичного трикутника довели математики середньовічного Сходу ще в X столітті[3]. У праці аль-Джайяні XI століття «Книга про невідомі дуги сфери» наводилось загальне доведення теореми синусів на сфері[4].

Див. також

Примітки

Florian Cajori. A History of Mathematics : [англ.]. — 5th edition. — 1991. — С. 47.
Berggren, J. Lennart. Mathematics in Medieval Islam // The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook : [англ.]. — Princeton University Press, 2007. — С. 518. — ISBN 9780691114859.
Sesiano just lists al-Wafa as a contributor. Sesiano, Jacques (2000). «Islamic mathematics», pp. 137. — Page 157, in Selin, Helaine; D'Ambrosio, Ubiratan (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer. ISBN 1402002602.
Abu Abd Allah Muhammad ibn Muadh Al-Jayyani

Посилання

Синусів теорема // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Florian Cajori. A History of Mathematics : [англ.]. — 5th edition. — 1991. — С. 47.

[2] Berggren, J. Lennart. Mathematics in Medieval Islam // The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook : [англ.]. — Princeton University Press, 2007. — С. 518. — ISBN 9780691114859.

[Sesiano-3] Sesiano just lists al-Wafa as a contributor. Sesiano, Jacques (2000). «Islamic mathematics», pp. 137. — Page 157, in Selin, Helaine; D'Ambrosio, Ubiratan (2000). Mathematics Across Cultures: The History of Non-western Mathematics. Springer. ISBN 1402002602.

[MacTutor_Al-Jayyani-4] Abu Abd Allah Muhammad ibn Muadh Al-Jayyani

Тригонометрія

Обрис Історія Застосування Функції (обернені) Узагальнена тригонометрія
Посилання
Тотожності Точні сталі Таблиці Одиничне коло
Закони і теореми
Синуси Косинуси Тангенси Котангенси Теорема Піфагора
Обчислення
Тригонометричні підстановки Інтеграли (обернені функції) Похідні