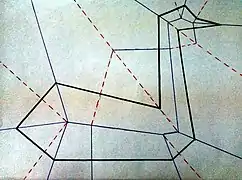
Теорема оригамі про вирізання многокутника

Теорема оригамі про вирізання многокутника стверджує, що завжди можна так скласти аркуш паперу, що будь-який многокутник, намальований на ньому (можливо не опуклий), можна отримати одним прямолінійним розрізом[1]

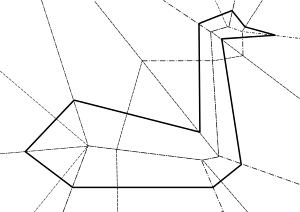
Патерн для многокутника у вигляді лебедя. Лінії «долина» позначені пунктирною лінією, лінії «гора» — штрих пунктирною

Теорема находить застосування в оригамі. Патерном в оригамі називають набір ліній і відрізків, що вказують на те, як згортати папір з кресленнями, щоб отримати задану форму. Слід звернути увагу, в якому напрямку рухається папір, при згині — лінія згину наближається до нас, чи навпаки віддаляється. Кажемо, що складка має назву гора, якщо лінія перегину наближається, і долина, якщо віддаляється.

Приклад

Послідовність основних кроків для вирізання однією лінією на прикладі багатокутника у вигляді фігури лебедя:

1 крок
1 крок 
2 крок
2 крок 
3 крок
3 крок 
4 крок
4 крок 
5 крок
5 крок 
6 крок
6 крок 
  1. Потрібно роздрукувати шаблон (паттерн). На малюнку позначені лінії «долина» — червоним кольором, лінії «гора» — блакитним.
  2. Усі лінії намічаються у потрібному напрямку: «долина» — до себе (лінія згину віддаляється), «гора» — від себе (лінія згину наближається). За межі намальованих ліній виходити не можна. Показаний згин «гора».
  3. Паттерн з усіма наміченими лініями.
  4. За усіма наміченими лініями проходить згин таким чином, щоб отримати одну лінію.
  5. За цією лінією робиться розріз.
  6. Обидві частини розгортаються. З аркушу паперу вирізаний лебідь, і отвір у аркуші лише у формі лебедя. Залишок аркушу цілий.

Теорема оригамі про вирізання многокутника фактично стверджує, що завжди можна створити паттерн, з якого можна отримати задану фігуру, розрізанням лише по одній лінії. Для цього існують різні методи, які наведені нижче.

Доведення теореми у випадку трикутника

Нехай потрібно отримати паттерн для вирізання по одній прямій заданого трикутника. Проведемо бісектриси та із точки їх перетину опустимо перпендикуляри на сторони трикутника. По цим прямим і будемо складати аркуш паперу. Усі сторони трикутника опиняються на одній прямій. Уздовж неї відбувається прямолінійний розріз. Таким чином буде отримано у відрізаній частині шуканий трикутник, а на аркуші, з якого вирізали, буде відповідний отвір у вигляді заданого трикутника.

Прямий скелетний метод
Метод прямолінійного скелету

Ерік Демейн, Мартін Демейн і Анна Лубів розв'язували задачу «розрізу і згинання» за допомогою прямолінійного скелету. Ця структура визначається (приблизно) наступним чином. Для кожної грані бажаної схеми розрізу (область між розрізами), зменшуємо сторону так, щоб краї залишалися паралельно і рухалися з постійною швидкістю в перпендикулярному напрямку. Зупиняємося, коли границя перетинає себе, й продовжуємо зменшувати кожну частину. Прямий скелет — це траєкторія руху вершин бажаного паттерну розрізу під час цього процесу зменшення. Прямолінійний скелет складається з більшості згинів і досягає бажаного «вибудовування в ряд» розрізів. Взагалі, з кожної вершини прямолінійного скелету проводять промінь, який перпендикулярний кожному досягнутому краю розрізу, промінь відбивається від будь-якої грані, що зустрічається.

Складною частиною є доказ того, що прямолінійний скелет згину разом з підмножиною перпендикулярних згинів (і декількома допоміжними згинами) може бути складено в пласке оригамі. Це робиться через показування положень складання, тобто за допомогою того, як шматочки паперу виглядають, коли складаються. Цей стан складання повинен задовольнити такої властивості: кожна сторона зберігає ізометрію і папір не повинен перетинати себе.

Найбільш детальний опис цього — книга «Геометрія алгоритмів складання: з'єднання, оригамі, багатогранники» Еріка Демейна і Джозефа О'Рурка.

Також цю проблему розглядав Роберт Ленг. Власне кажучи, він намагається згорнути многокутник в спеціальну згорнуту форму, але звертається лише до опуклих многокутників, у той час, коли метод прямолінійного скелету зосереджується на розгортанні форми й звертається до неопуклих й незв'язних многокутників.

Метод пакування диска
Метод пакування диска

Маршал Берн, Девід Енштайн, Баррі Хайес і Ерік Демейн розв'язували задачу «розрізу і згинання» використовуючи пакування диска. А саме розміщували диски на частині паперу так, що:

  1. Диски не заходять один на одного (але можуть торкатися);
  2. Проміжки між дисками мають або три, або чотири боки;
  3. Є диск з центром у кожній вершині бажаної схеми розрізу;
  4. Краї бажаної схеми розрізу — об'єднання радіусів дисків.

Внаслідок цього, можна розкласти бажаний паттерн розрізу за допомогою ребер між центрами дисків, що торкаються. Результатом цього є колекція трикутників і чотирикутників. Після цього потрібно скласти усі ці трикутники і чотирикутники використовуючи точки, що вибудовуються у ряд по границі трикутників і чотирикутників. Це головна ідея — пара особливостей, необхідних за для того, щоб показати, що точки можуть бути з'єднані разом. Подальша особливість полягає в тому, щоб показати, що тільки бажані лінії такі, що проходять разом на загальній лінії.

Найбільш детально це описано у книзі «Геометрія алгоритмів складання: з'єднання, оригамі, багатогранники». «Методи пакування диска для магії оригамі» також описують детально методи, але вона має маленькі проблеми. Сама остання версія включає деякі спрощення і з'явилася в працях Третьої міжнародної зустрічі наукового оригамі, математики й освіти. Оригінальна версія була опублікована в працях Міжнародної конференції веселих алгоритмів.

Див. також

Примітки
  1. Demaine, Erik D.; Demaine, Martin L. (2004). Fold-and-Cut Magic. Tribute to a Mathemagician. A K Peters. с. 23–30..

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.