Теорія гравітації Лесажа
У 1690 році женевський математик[1] Нікола Фатіо де Дюйє, а згодом в 1756 Жорж Луї Лесаж в Женеві запропонували просту кінетичну теорію гравітації, яка дала механічне пояснення рівняння сили Ньютона.[2] Через те, що робота Фатіо була широко відома і залишалася неопублікованою тривалий час, саме опис теорії Ле Сажем став темою підвищеного інтересу в кінці XIX століття, коли дана теорія була вивчена в контексті щойно відкритої кінетичної теорії газів[3]. Таке механічне пояснення гравітації ніколи не отримувало широкого визнання і до початку XX століття теорія в цілому вважалася спростованою, в основному через проблеми, підняті Максвеллом[4], Пуанкаре.[5] Крім того, у другому десятилітті XX століття Альберт Ейнштейн створив загальну теорію відносності, але, визнання до неї прийшло дещо пізніше. Хоча теорія Ле Сажа все ще розробляється деякими дослідниками, вона зазвичай не розглядається основним науковим співтовариством як життєздатна теорія та становить переважно історичний інтерес.
Основна теорія
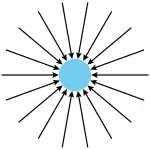
Немає чистої спрямованої сили
Природа гравітації
Теорія стверджує, що сила гравітації — це результат руху крихітних частинок, що рухаються з великою швидкістю у всіх напрямках у Всесвіті. Інтенсивність потоку частинок в усіх напрямках передбачається однаковою, таким чином, ізольований об'єкт A вдаряється частинками з усіх боків, в результаті чого він піддається тиску всередину об'єкта, але не піддається спрямованій силі P1.

Однак, в разі присутності другого об'єкта B, частина частинок, які б ударили по об'єкту A з боку B, перехоплюється, в такому випадку B працює як екран, адже з напряму В об'єкт A вдарить менше кількість частинок, ніж з протилежного напрямку. Аналогічно, об'єкт B буде вдарений меншою кількістю частинок з боку A, в порівнянні з протилежною стороною. Тобто, можна сказати, що об'єкти A і B «екранують» один одного, і обидва тіла притискаються один до одного результуючим дисбалансом сил (P2). Таким чином, здається, що тяжіння між тілами в даній теорії насправді є зменшене тиском на тіло з боку інших тіл. З цієї причини цю теорію іноді називають «push гравітація» або «тіньова гравітація», хоча найчастіше зустрічається назва «гравітація Лесажа».
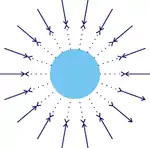
Якщо зіткнення тіла A і гравітаційної частинки цілком пружне, інтенсивність відбитих частинок буде настільки ж сильною, як і тих частинок, що приходять тобто чиста спрямована сила не виникне. Дане твердження вірне і в тому випадку, якщо ми введемо друге тіло В, яке буде діяти як екран для гравітаційних частинок в напрямку тіла A. Гравітаційна частка C, яка в звичайній ситуації вдарила б по об'єкту A, блокується В, але інша частка D, яка в звичайній ситуації не вдарила б по A, перенаправляється пружним відбиттям від об'єкта B на об'єкт A, і отже замінює C. Таким чином, якщо зіткнення цілком пружне, відбиті частинки між об'єктами A і B повністю компенсують будь-який «екрануючий» ефект. Щоб пояснити суть гравітаційної сили, ми повинні припустити, що зіткнення частинок не є повністю пружним, або хоча б те що відбиті частинки сповільнюються, адже їх імпульс зменшується після зіткнення. Це призведе до того що від об'єкта А відходить потік зі зменшеним імпульсом, а приходить потік з незміненим імпульсом, таким чином з'являється чистий спрямований імпульс до центру об'єкта A (P3). Якщо прийняти це припущення, то відбиті частки у випадку 2 взаємодіючих тіл, повністю не компенсують ефект екрану, через те, що відбитий потік слабший, ніж падаючий на тіло потік.
Обернено-квадратична залежність
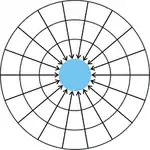
З припущення, що деякі (або всі) гравітаційні частинки, що сходяться на об'єкті, абсорбуються або сповільнюються цим об'єктом, слідує, що інтенсивність потоку гравітаційних частинок, що випускається від більшого об'єкта, менша ніж інтенсивність потоку, що падає на цей об'єкт. Можна припустити, що цей дисбаланс імпульсу потоку і відповідно сили прикладеної на будь-яке тіло поблизу об'єкта, розподілений по сферичній поверхні з центром на даному об'єкті (P4). Дисбаланс імпульсу потоку над усією сферичною поверхнею, яка оточує об'єкт, не залежить від розміру навколишньої сфери, в той же час площа поверхні сфери збільшується пропорційно квадрату радіуса. Отже, дисбаланс імпульсу на одиницю площі зменшується в обернено-квадратичній залежності від відстані.
Пропорційність масі
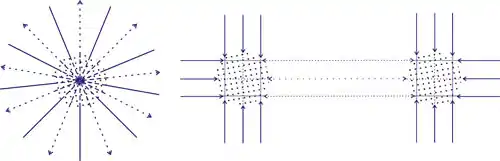
З фактів, наведених вище, слідує, що виникає сила, прямо пропорційна тільки поверхні тіла. Але сила гравітації пропорційна також масам. Щоб задовольнити необхідність в пропорційності від маси, теорія стверджує, що: а) базові елементи матерії дуже малі, таким чином, матерія в основному складається з порожнього простору; б) що гравітаційні частинки настільки малі, що лише дуже мала частина з них перехоплюється матерією. В результаті чого, «тінь» кожного тіла прямо пропорційна поверхні кожного з базових елементів матерії. Якщо тепер припустити, що елементарні непрозорі (для гравітаційних частинок) елементи всієї матерії ідентичні (мають таке ж відношення щільності до поверхні), то з цього випливає, що ефект екрана (хоча б приблизно) пропорційний масі (P5).
Ранній розвиток теорії
Фатіо
Фатіо представив перше формулювання своїх думок про гравітації в листі до Гюйгенса навесні 1690 року.[1] Два дні по тому він зачитав зміст листа перед Лондонським Королівським товариством . У наступні роки Фатіо написав кілька чорнових рукописів своєї головної праці «De la Cause de la Pesanteur». Деякі фрагменти цих рукописів були в подальшому придбані Ле Сажем (див. Нижче) і були знайдені розкиданими серед паперів Ле Сажа в 1944 році. На підставі цих фрагментів і конспекта, зробленого самим Фатіо, Бернар Ганєбен спробував відновити праці Фатіо.[6] Ганєбен не знав, що повна копія одної з ранніх чернеток, написаних в 1701 році, була знайдена Карлом Боппом в 1915 році серед паперів сім'ї Бернуллі і лягла в основу видання праці Фатіо, опублікована Боппом в 1929 році.[7] Видання Боппа більш докладне, ніж видання Ганєбена, але видання Ганєбена включає в себе виправлення зроблені Фатіо до 1743 року включно, на 40 років пізніше створення чернетки, на якій ґрунтується видання Боппа. Для детального аналізу праці Фатіо і порівнянням між виданнями Боппа і Ганєбена — дивіться публікації Цехе.[8] Нижче приведений опис в основному базується на виданні Боппа. Вони були названі Фатіо «Проблеми I—IV», в той же час між Проблемою I і проблемою II формулюється 5 теорем. Проблеми II—IV складають другу половину видання Боппа і містять математичні найпередовіші ідеї теорії Фатіо, але вони не були включені Ганєбеном в його видання праць Фатіо.
Деякі властивості теорії Фатіо

Піраміда Фатіо (Проблема I):[9] Фатіо припустив, що всесвіт наповнений дрібними корпускулами, які рухаються з дуже високою швидкістю хаотично і прямолінійно в усіх напрямках. Щоб проілюструвати свої думки, він використовував наступний приклад: Уявімо об'єкт С, на якому розташована нескінченно маленька площину zz і намальована сфера з центром в zz. У цю сферу Фатіо помістив піраміду PzzQ, в якій деякі корпускули рухаються в напрямку zz, а також деякі корпускули, які вже були відображені об'єктом C і, отже, залишають площину zz. Фатіо припустив, що середня швидкість відбитих частинок менша і отже імпульс менший ніж у падаючих на тіло корпускул. В результаті виходить один потік, який штовхає все тіла у напрямку до zz. Таким чином, з одного боку швидкість потоку залишається постійною, але з іншого боку при більшій близькості до zz щільність потоку збільшується і отже його інтенсивність пропорційна 1/r 2. А оскільки можна намалювати нескінченну кількість таких пірамід навколо C, то пропорційність 1/r 2 застосовні до всієї області навколо C.
Зменшена швидкість: щоб підтвердити припущення, що корпускули після відображення рухаються зі зменшеними швидкостями, Фатіо зробив наступні припущення:[10] a) звичайна речовина або гравітаційні корпускули, або і те й інше — непружні; б) зіткнення повністю пружні, але корпускули не абсолютно тверді, і отже переходять в стан коливання після зіткнення і (або) c) через тертя корпускули починають обертатися після зіткнення. Ці уривки теорії Фатіо — найменш зрозумілі, бо він ніколи точно не вирішив, який з варіантів зіткнень найкращий.[11] Однак, в останній версії своєї теорії в 1742 році він скоротив пов'язані уривки і написав «повна пружність або сила пружності» для корпускул і «неповна пружність» для звичайної речовини, отже корпускули повинні бути відображені зі зменшеними швидкостями.[12]До того ж, Фатіо зіткнувся з іншою проблемою: що відбувається, коли корпускули стикаються одна з одною? Непружне зіткнення призводить до постійного зменшення швидкості корпускул і отже до зменшення гравітаційної сили. Щоб уникнути цієї проблеми, Фатіо припустив, що діаметр корпускул дуже малий у порівнянні з відстанню між ними, таким чином, взаємодії між корпускулами відбуваються дуже рідко.
Конденсація:[13] щоб пом'якшити протиріччя, які виникли через те, що чим менша швидкість корпускул, тим більше корпускул буде акумулюватися біля тіл, Фатіо припустив, що корпускули відображаються в піраміду TzzV. У той же час, якщо корпускули приходять з боку PQ досягають C, то відбиті частки не досягають TV, а прибувають в tu. Однак, це не призводить до нескінченного накопичення частинок, а тільки до конденсації, позаяк збільшена щільність залишається незмінною. Фатіо вказав на те, що, продовжуючи збільшувати швидкість, Tt може стати скільки завгодно малим по відношенню до TZ.

Пористість звичайної речовини:[14] щоб забезпечити пропорційність масі, Фатіо припустив, що звичайне речовина, має надзвичайну проникність для гравітаційної рідини (потоку корпускул). Він зробив зразки 3 моделей, щоб підтвердити своє припущення. a) Фатіо припустив, що матерія складається з маленьких «кульок», діаметр яких порівняно з відстанню між ними «нескінченно» малий. Але він відкинув це припущення, на підставі того, що при таких умовах «кульки» будуть прагнути один до одного, і тіло не буде залишатися «стабільним». б) Після цього він зробив припущення, що «кульки» можуть бути з'єднані лініями або прутами, і формують в деякому роді кристалічну решітку. Однак він визнав непридатною і цю модель теж. Якщо деякі атоми знаходяться поруч один з одним, то гравітаційна рідина не зможе проникнути в цю структуру однаково з усіх сторін, і відповідно пропорційність масі неможлива. в) В кінці кінців, Фатіо прибрав і «кульки», залишивши тільки лінії або сітку, зробивши лінії «нескінченно» меншими в порівнянні з відстанню між ними, досягнувши таким чином максимальної проникливої здібності.
Сила тиску корпускул (Проблема II):[15] Вже в 1690 році Фатіо припустив, що «штовхальна сила», що викликається корпускулами на рівній площині, в 6 разів менша, ніж сила, яка була б створена цими ж корпускулами, якби вони були розташовані по нормалі до поверхні. Фатіо наводить доказ свого припущення, шляхом визначення сили, яка викликається корпускулами на певній точки площині zz. Він виводить формулу p = ρ v²zz/6. Це рішення дуже схоже на формулу відому в кінетичної теорії газів p = ρ v²/3, яка була виведена Даніелем Бернуллі в 1738 році. Це перший раз, коли спостерігається близька аналогія між таким видом гравітаційних теорій і кінетичної теорії газів — задовго до розвитку базових концепцій більш пізньої з теорій. Однак значення, отримане Бернуллі, в 2 рази більше, ніж значення Фатіо, тому що (відповідно з Цехе) Фатіо розрахував тільки значення mv для зміни імпульсу після зіткнення, а не 2mv і, отже, отримав неправильний результат (його результат вірний тільки для повністю непружного зіткнення). Фатіо намагався використовувати своє рішення не тільки для пояснення гравітації, але також і для пояснення поведінки газів. Він спробував сконструювати термометр, який повинен був показувати «стан руху» молекул повітря і, отже, підраховувати температуру. Але Фатіо (на відміну від Бернуллі) не ідентифікува теплоту з рухом частинок повітря, він використовував іншу рідину, яка повинна нести відповідати за цей ефект.[16] Також не відомо, чи праці Фатіо мали вплив на Бернуллі чи ні.
Нескінченність (Проблема III):[17] У цьому розділі Фатіо досліджує зв'язок між поняттям «нескінченність» і її запровадженням до своєї теорії. Фатіо часто пояснював свої припущення тим фактом, що різні явища «нескінченно менші або нескінченно більші» ніж інші, і таким чином багато проблем можуть бути зменшені до невизначеного значення. Наприклад, діаметр «перегородок» «нескінченно менший», ніж відстань між ними або що швидкість корпускул «нескінченно більша», ніж у звичайної речовини або різниця в швидкості між відбитими або невідображеними корпускулами «нескінченно маленька».
Опір середовища (Проблема IV):[18] Це математично найскладніша частина теорії Фатіо. Тут він намагається оцінити опір потоку корпускул тілам, що рухаються. Припустимо, що u — швидкість звичайної речовини, v — швидкість гравітаційних частинок і ρ — густота середовища. У разі якщо v << u і ρ = const, Фатіо зробив висновок що опір дорівнює ρu2. У разі якщо v >> u і ρ = const, опір дорівнює 4/3 ρuv. У цьому місці Ньютон констатував, що відсутність опору орбітальному руху планет вимагає надзвичайної розрідженості будь-якого середовища в космосі. Тому Фатіо зменшив густоту середовища і заявив, що щоб зберегти достатню гравітаційну силу, це зменшення повинно бути компенсоване зміною v «обернено пропорційе кореню квадратному густоти». Це випливає з корпускулярного тиску Фатіо, який пропорційний ρv2. Відповідно до Цехе, ідея Фатіо збільшити v до дуже великих значень дійсно зробить опір дуже маленьким в порівнянні з гравітацією (і взагалі як завгодно маленьким) через те, що опір в моделі Фатіо пропорційний ρuv, а гравітація (тобто тиск корпускул) пропорційна ρv2.
З іншого боку, сам Фатіо заявляв, що хоча Ньютон особисто прокоментував, що теорія Фатіо є найкращим можливим механічним поясненням гравітації, він також визнавав, що Ньютон схилявся до ідеї, що дійсна причина тяжіння перестає бути механічною. Також, Д. Грегорі зробив замітку в своїй «Memoranda» «Містер Ньютон і містер Галлей сміялися над манерою викладу гравітації Фатіо». Це нібито було позначено ним 28 грудня 1691 року. Однак, справжня дата невідома, бо і використані чорнило і перо відрізняються від решти сторінки.[19] Після 1694 року відносини між двома вченими охололи.
Думки Ньютона про теорію Фатіо дуже різняться. Наприклад, після опису необхідних умов механічного пояснення гравітації, в 1692 році він написав в (неопублікованій) записці у своїй власній копії «Principia»:
Унікальна гіпотеза, яка може пояснити гравітацію, була розроблена найгеніальнішим геометром, містером Н. Фатіо.[20]
Гюйгенс був першою людиною, яку Фатіо поінформував про свою теорію, але він ніколи не визнавав теорію вірною. Фатіо вірив, що переконав Гюйгенса в спроможності своєї теорії, але Гюйгенс спростував це в своєму листі до Лейбніца.[21] Також існувало коротке листування про теорію між Фатіо і Лейбніцем. Лейбніц критикував теорію Фатіо за існування порожнього простору між частинками, існування якого заперечувалося Лейбніцом на філософської грунті.[22] Якоб Бернуллі виявив інтерес до теорії Фатіо, і спонукав Фатіо записати свої думки про гравітації в завершеному рукописі, що і було зроблено Фатіо. Бернуллі після цього скопіював рукопис, який тепер знаходиться в бібліотеці університета в Базеля, і на якому започатковано видання Боппа.[23]
Проте, теорія Фатіо залишалася в основному невідомою (крім деяких винятків, наприклад Крамера і Лесажа) через те, що a) він ніколи не зміг формально опублікувати свої роботи і б) він потрапив під вплив групи релігійних фанатиків, які називалася «Французькі пророки»(«French prophets»), що належала до французької протестантської течією камізарів (camisards), які підняли повстання проти релігійних переслідувань у Франції в цей історичний період, і його публічна репутація була підірвана.
Крамер, Редекер
У 1731 році швейцарський математик Габріель Крамер опублікував дисертацію,[24] в кінці якої з'явився нарис теорії абсолютно схожої на теорію Фатіо (включаючи «сіткоподібну» структуру речовини, аналогію зі світлом, екрануванням і т. д.), але без згадки імені Фатіо. Фатіо було відомо, що Крамер мав доступ до копії його головної роботи, так що він звинуватив Крамера в плагіаті теорії без розуміння її. Крамер також поінформував Лесажа про теорію Фатіо в 1749 році. У 1736 році німецький лікар Редекер теж публікує схожу теорію.[25] Відповідно до Превостом, Редекер припустив, що частинки в його моделі абсолютно непружні, але не дав точного аналізу феномена. Чи існував зв'язок між Фатіо і Редекера — невідомо.[26]
Ле Саж
Перший опис своєї теорії Essai sur l'origine des forces mortes, був відправлений Лесажем в Паризьку Академію наук в 1748 році, але він ніколи не був опублікований (с. 154—158). Так, за словами Лесажа після створення і відправки свого есе, він був проінформований про теорії Фатіо, Крамера і Редекера. Тільки в 1756 році в перший раз один з описів його теорії було опубліковано.[27] А вже в 1758 році він відправив більш детальний опис теорії Essai de Chymie Méchanique (Тест механічної хімії), на конкурс до Академії наук Руана.[28] У цій праці він намагався пояснити як природу гравітації так і сили хімічного тяжіння. Опис теорії, який став доступним широкому загалу називався Lucrèce Newtonien (Лукреція ньютонівська), в цьому описі було розкрито відповідність даної теорії з уявленнями Лукреція.[29] Ще одн опис теорії із записів Лесажа було опубліковано після смерті автора в 1818 році П'єром Прево.[30]
Критика
Критики теорії Лесажа відзначали безліч її слабких місць, особливо з точки зору термодинаміки. Джеймс Максвелл показав, що в моделі Лесажа енергія неодмінно перейде в теплову і швидко розплавить будь-яке тіло. Анрі Пуанкаре підрахував (1908), що швидкість корпускул повинна бути на багато порядків вище швидкості світла, і їх енергія спопелила б всі планети[31]. Були відзначені і непереборні логічні труднощі[32]:
- Якщо тяжіння викликане екрануванням, то Місяць в ті моменти, коли він знаходиться між Землею і Сонцем, повинен істотно впливати на силу тяжіння цих тіл і, відповідно, на траєкторію Землі, проте нічого подібного в реальності не спостерігається.
- Тіло, яке швидко рухається, повинне зазнавати попереду надлишкового тиску з боку корпускул.
Спроба Джорджа Дарвіна замінити корпускули на хвилі в ефірі виявилася також невдалою. В огляді в 1910 році модель Лесажа впевнено характеризується як неспроможна.
Див. також
Література
- Богородский А. Ф. Всемирное тяготение. — Киев : Наукова думка, 1971. — 351 с.
- Роузвер Н. Т. Перигелий Меркурия. От Леверье до Эйнштейна = Mercury's perihelion. From Le Verrier to Einstein. — М. : Мир, 1985. — 244 с.
Примітки
- Fatio, 1690a
- Le Sage, 1756
- Thomson, W. 1873
- Maxwell и 1875
- Poincaré, 1908
- Fatio, 1743
- Fatio, 1701
- Zehe, 1980
- Fatio, 1690a; Fatio, 1701, pp. 32-35; Zehe, 1980, pp. 134—156
- Fatio, 1690a; Fatio, 1701, p. 34;
- Zehe, 1980, pp. 198—204.
- Zehe, 1980, p. 385; Fatio, 1743, pp. 134—135.
- Fatio, 1690a, p. 387; Fatio, 1690c, pp. 38-39;
- Fatio, 1701, pp. 36-38 and 59-61; Zehe, 1980, pp. 206—214.
- Fatio, 1701, pp. 47-49; Zehe, 1980, pp. 227—241 and 198—205
- Zehe, 1980, p. 239
- Fatio, 1701, pp. 49-50; Zehe, 1980, pp. 242—254.
- Fatio, 1701, pp. 50-64. Zehe, 1980, pp. 255—276.
- Zehe, 1980, p. 374.
- Newton, in Latin:«Hiijus autem generis Hypothesis est unica, per quam Gravitas explicari potest, eamque Geometra Ingeniossimus Pr. Fatius primus excogitavit.»; Fatio-c, p. 65;
- Zehe, 1980, p. 176
- Zehe, 1980, pp. 173—175
- Fatio, 1701, pp. 19-20
- Cramer, 1731
- Redeker, 1736
- Le Sage, 1818, pp. XXXI—XXXII
- Le Sage, G.-L. (1756). Letter à une académicien de Dijon.... Mercure de France: 153–171.
- Le Sage, G.-L. (1761). Essai de Chymie Méchanique. Not published - private print.
- Le Sage, G.-L. (1784). Lucrèce Newtonien. Memoires de l’Academie Royale des Sciences et Belles Lettres de Berlin: 404–432. An English translation appears in Le Sage, G.-L. (1898). The Newtonian Lucretius. У Langley, Samuel P.. The Le Sage theory of gravitation. Annual Report of the Board of Regents of the Smithsonian Institution (June 30, 1898): 139–160.
- Le Sage, G.-L. (1818). Physique Mécanique des Georges-Louis Le Sage. У Prévost, Pierre. Deux Traites de Physique Mécanique. Geneva & Paris: J.J. Paschoud. с. 1–186. Архів оригіналу
|archiveurl=вимагає|url=(довідка) за 26 червня 2015. - Роузвер Н. Т., 1985, с. 133—138..
- Богородский А. Ф., 1971, с. 31—34.
