Формула Бретшнайдера
У геометрії формулою Бретшнайдера є наступний вираз для обчислення площі загального чотирикутника :
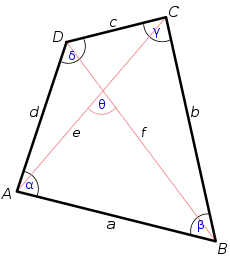
Тут a , b , c , d - сторони чотирикутника, p - півпериметр , а α і γ - два протилежні кути.
Формулу Бретшнайдера можна застосовувати для обчислення площі будь-якого чотирикутника.
Німецький математик Карл Антон Бретшнайдер відкрив формулу в 1842 році. У тому ж році формулу отримав і німецький математик Карл Георг Крістіан фон Штаудт.
Доведення
Позначимо площу чотирикутника за S. Тоді ми маємо
Тому
З теореми косинусів випливає, що
оскільки обидві сторони дорівнюють квадрату довжини діагоналі BD. Це можна записати як
Додавання цього до вищенаведеної формули для 4S2 дає
Зауважте, що: (тригонометрична тотожність правильна для всіх )
Слідуючи тими ж кроками, що й у формулі Брахмагупти, це можна записати так
Введемо півпериметр
отримуємо
формула Бретшнайдера випливає після взяття квадратного кореня з обох сторін:
Пов'язані формули
Формула Бретшнайдера узагальнює формулу Брахмагупти для площі вписаного чотирикутника, яка у свою чергу узагальнює формулу Герона для площі трикутника.
Тригонометричне перетворення у формулі Бретшнайдера для невписаного чотирикутника може бути подано нетригонометрично в термінах сторін та діагоналей e та f [1] [2]
Примітки
- JL Coolidge, "Цікаві формули для обчислення площі чотирикутника", American Mathematical Monthly , 46 (1939) 345–347. ( JSTOR )
- EW Hobson : Трактат про плоску тригонометрію . Cambridge University Press, 1918, с. 204-205
Посилання та подальше читання
- Аюб Б. Аюб: Узагальнення теорем Птолемея і Брахмагупти . Математика та комп'ютерна освіта, том 41, № 1, 2007, ISSN 0730-8639
- EW Hobson : Трактат про плоску тригонометрію . Cambridge University Press, 1918, с. 204–205 ( онлайн-копія )
- CA Bretschneider. Untersuchung der trigonometrischen Relationen des geradlinigen Viereckes. Архітектура математики і фізики, група 2, 1842, с. 225-261 ( електронна копія, німецька )
- F. Strehlke: Zwei neue Sätze vom ebenen і sphärischen Viereck і Umkehrung des Ptolemaischen Lehrsatzes . Архітектура математики і фізики, група 2, 1842, с. 323-326 ( електронна копія, німецька )
Зовнішні посилання
- Weisstein, Eric W. Bretschneider's formula(англ.) на сайті Wolfram MathWorld.
- Bretschneider's formula на proofwiki.org