Інтегральна показникова функція

Для дійсних або комплексних аргументів, які знаходяться поза від'ємною дійсною віссю, ${\displaystyle \operatorname {E} _{1}(z)}$ може бути виражений як[4]

${\displaystyle \operatorname {E} _{1}(z)=-\gamma -\ln {z}-\sum _{k=1}^{\infty }{\frac {{(-z)}^{k}}{kk!}},\qquad |\operatorname {Arg} (z)|<\pi ,}$

де ${\displaystyle \gamma }$ — константа Ейлера–Маскероні. Ряд збігається для всіх комплексних ${\displaystyle z}$, і ми беремо звичайне значення комплексного логарифму, який має розгалуження вздовж від'ємної дійсної осі.

Ця формула може бути використана для обчислення ${\displaystyle \operatorname {E} _{1}(x)}$ в операціях з плаваючою комою для дійсного ${\displaystyle x}$ між ${\displaystyle 0}$ та ${\displaystyle 2{,}5}$. Для ${\displaystyle x>2{,}5}$ результат неточний через втрату значущості.

Ряд який збігається швидше знайшов Рамануджан:

${\displaystyle \operatorname {Ei} (x)=\gamma +\ln {x}+\exp \left({\frac {x}{2}}\right)\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}x^{n}}{n!2^{n-1}}}\sum _{k=0}^{\lfloor (n-1)/2\rfloor }{\frac {1}{2k+1}}.}$

Даний збіжний ряд може використовуватися для отримання асимптотичних оцінок, наприклад,

${\displaystyle 1-{\frac {3x}{4}}\leq \operatorname {Ei} (x)-\gamma -\ln {x}\leq 1-{\frac {3x}{4}}+{\frac {11x^{2}}{36}}}$

для ${\displaystyle x\geq 0}$.

Відносна похибка асимптотичного наближення для різного числа ${\displaystyle N}$ доданків в усічений сумі (${\displaystyle N=1}$ — червона лінія, ${\displaystyle N=5}$ — рожева лінія).

На жаль, збіжність рядів що наведені вище є повільною для великих за модулем аргументів. Наприклад, для ${\displaystyle x=10}$ потрібно більше 40 членів, щоб для ${\displaystyle \operatorname {E} _{1}(z)}$ отримати у відповіді перші три правильні цифри.[5] Однак існує апроксимація розбіжним рядом, який можна отримати інтегруючи ${\displaystyle ze^{z}\operatorname {E} _{1}(z)}$ частинами:[6]

${\displaystyle \operatorname {E} _{1}(z)={\frac {\exp(-z)}{z}}\sum _{n=0}^{N-1}{\frac {n!}{(-z)^{n}}}}$

з похибкою порядку ${\displaystyle O{\big (}N!z^{-N}{\big )}}$ і яка може використовуватися при великих значень ${\displaystyle \operatorname {Re} (z)}$. Відносна похибка такої апроксимації приблизно зображена на рисунку (для різних значень ${\displaystyle N}$ кількості доданків у сумі).

Двостороння оцінка ${\displaystyle \operatorname {E} _{1}}$ елементарними функціями.

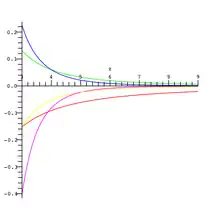
З двох рядів, які показані в попередніх підрозділах випливає, що ${\displaystyle \operatorname {E} _{1}}$ поводить себе як від'ємна експонента для великих значень аргументу, і як логарифм — для малих значень. Для додатних дійсних значень аргументу ${\displaystyle \operatorname {E} _{1}}$ можна обмежити елементарними функціями наступним чином[7]:

${\displaystyle {\frac {1}{2}}{\rm {e}}^{-x}\ln \left(1+{\frac {2}{x}}\right)<\operatorname {E} _{1}(x)<{\rm {e}}^{-x}\ln \left(1+{\frac {1}{x}}\right),\qquad x>0.}$

На рисунку ліва частина цієї нерівності зображена синім кольором, центральна частина ${\displaystyle \operatorname {E} _{1}(x)}$ позначена чорним кольором, а права частина нерівності — червоним.

Функції ${\displaystyle \operatorname {Ei} }$ і ${\displaystyle \operatorname {E} _{1}}$ можна записати простіше, використовуючи цілу функцію ${\displaystyle \operatorname {Ein} }$[8], визначену як

${\displaystyle \operatorname {Ein} (z)=\int \limits _{0}^{z}(1-{\rm {e}}^{-t})\,{\frac {{\rm {d}}t}{t}}=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}z^{k}}{kk!}}}$

(зауважте, що це лише знакозмінний ряд у наведеному вище означенні ${\displaystyle \operatorname {E} _{1}}$). Тоді

${\displaystyle \operatorname {E} _{1}(z)=-\gamma -\ln {z}+\operatorname {Ein} (z),\qquad |\operatorname {Arg} (z)|<\pi ,}$

${\displaystyle \operatorname {Ei} (x)=\gamma +\ln {x}-\operatorname {Ein} (-x),\qquad x>0.}$

Диференціальне рівняння Куммера

${\displaystyle z{\frac {{\rm {d}}^{2}w}{{\rm {d}}z^{2}}}+(b-z){\frac {{\rm {d}}w}{{\rm {d}}z}}-aw=0}$

як правило, розв'язується за допомогою вироджених гіпергеометричних функцій ${\displaystyle M(a,b,z)}$ та ${\displaystyle U(a,b,z)}$. Але при ${\displaystyle a=0}$ та ${\displaystyle b=1}$ рівняння набуває вигляду

${\displaystyle z{\frac {{\rm {d}}^{2}w}{{\rm {d}}z^{2}}}+(1-z){\frac {{\rm {d}}w}{{\rm {d}}z}}=0,}$

і для всіх ${\displaystyle z}$

${\displaystyle M(0,1,z)=U(0,1,z)=1}$.

Другий розв'язок подається через ${\displaystyle \operatorname {E} _{1}(-z)}$. А саме,

${\displaystyle \operatorname {E} _{1}(-z)=-\gamma -i\pi +{\frac {\partial [U(a,1,z)-M(a,1,z)]}{\partial a}}{\bigg |}_{a=0},\qquad 0<\operatorname {Arg} (z)<2\pi }$.

Інший зв'язок з виродженими гіпергеометричними функціями полягає в тому, що ${\displaystyle \operatorname {E} _{1}}$ — це добуток експоненціальної функції та ${\displaystyle U(1,1,z)}$:

${\displaystyle \operatorname {E} _{1}(z)={\rm {e}}^{-z}U(1,1,z)}$.

Експоненційний інтеграл тісно пов'язаний з логарифмічною інтегральною функцією ${\displaystyle \operatorname {li} (x)}$ за допомогою формули

${\displaystyle \operatorname {li} ({\rm {e}}^{x})=\operatorname {Ei} (x)}$

для ненульових дійсних значень ${\displaystyle x}$.

Експоненційний інтеграл можна також узагальнити до функції

${\displaystyle \operatorname {E} _{n}(x)=\int \limits _{1}^{\infty }{\frac {{\rm {e}}^{-xt}}{t^{n}}}\,{\rm {d}}t}$,

яку можна записати як частковий випадок неповної гамма-функції [9]:

${\displaystyle \operatorname {E} _{n}(x)=x^{n-1}\Gamma (1-n,x)}$.

Таку узагальнену форму іноді називають функцією Мізра[10], ${\displaystyle \varphi _{m}(x)}$, що визначається як

${\displaystyle \varphi _{m}(x)=\operatorname {E} _{-m}(x)}$.

З використанням логарифму визначає узагальнену інтегро-експоненціальну функцію[11]

${\displaystyle \operatorname {E} _{s}^{j}(z)={\frac {1}{\Gamma (j+1)}}\int \limits _{1}^{\infty }(\log {t})^{j}{\frac {{\rm {e}}^{-zt}}{t^{s}}}\,{\rm {d}}t}$.

Невизначений інтеграл

${\displaystyle \operatorname {Ei} (a\cdot b)=\iint {\rm {e}}^{ab}{\rm {d}}a\,{\rm {d}}b}$

за формою схожий на звичайну твірну функцію для ${\displaystyle {\rm {d}}(n)}$, кількість дільників числа ${\displaystyle n}$:

${\displaystyle \sum _{n=1}^{\infty }{\rm {d}}(n)x^{n}=\sum _{a=1}^{\infty }\sum _{b=1}^{\infty }x^{ab}}$.

Похідні узагальнених функцій ${\displaystyle \operatorname {E} _{n}}$ можна обчислювати за формулою[12]:

${\displaystyle \operatorname {E} '_{n}(z)=-\operatorname {E} _{n-1}(z),\qquad n=1,2,3,\dots }$.

Зауважимо, що функція ${\displaystyle \operatorname {E} _{0}}$ — це просто ${\displaystyle {\rm {e}}^{-z}/z}$[13], і таким чином таке рекурсивне співвідношення досить зручне.

Графік дійсної (чорна крива) та уявної (червона крива) частин функції ${\displaystyle \operatorname {E} _{1}(ix)}$.

Якщо ${\displaystyle z}$ є уявним та має невід'ємну дійсну частину, то можна використовувати формулу

${\displaystyle \operatorname {E} _{1}(z)=\int _{1}^{\infty }{\frac {{\rm {e}}^{tz}}{t}}\,{\rm {d}}t}$

для співвідношення з тригонометричними інтегралами ${\displaystyle \operatorname {Si} }$ та ${\displaystyle \operatorname {Ci} }$:

${\displaystyle \operatorname {E} _{1}(ix)=i\left[-{\frac {1}{2}}\pi +\operatorname {Si} (x)\right]-\operatorname {Ci} (x),\qquad x>0}$.

Дійсні та уявні частини функції ${\displaystyle \operatorname {E} _{1}(ix)}$ зображені на рисунку.

Існує ряд наближень для експоненціальної інтегральної функції. Зокрема,

• Наближення Сваме та Охії[14]

${\displaystyle \operatorname {E} _{1}(x)=\left(A^{-7{,}7}+B\right)^{-0{,}13}}$,

де

${\displaystyle A=\ln \left[\left({\frac {0{,}56146}{x}}+0{,}65\right)(1+x)\right]}$,

${\displaystyle B=x^{4}{\rm {e}}^{7{,}7x}(2+x)^{3{,}7}}$.

• Наближення Аллена та Гастінгса[15]

${\displaystyle \operatorname {E} _{1}(x)={\begin{cases}-\ln {x}+{\boldsymbol {a}}{\boldsymbol {x}}_{5},\qquad x\leq 1,\\{\dfrac {{\rm {e}}^{-x}}{x}}{\dfrac {{\boldsymbol {b}}{\boldsymbol {x}}_{3}}{{\boldsymbol {c}}{\boldsymbol {x}}_{3}}},\qquad x\geq 1,\end{cases}}}$

де

${\displaystyle {\boldsymbol {a}}\triangleq [-0{,}57722,\,0{,}99999,\,-0{,}24991,\,0{,}05519,\,-0{,}00976,\,0{,}00108],}$

${\displaystyle {\boldsymbol {b}}\triangleq [0{,}26777,\,8{,}63476,\,18{,}05902,\,8{,}57333],}$

${\displaystyle {\boldsymbol {c}}\triangleq [3{,}95850,\,21{,}09965,\,25{,}63296,\,9{,}57332],}$

${\displaystyle {\boldsymbol {x}}_{k}\triangleq \left[x^{0},x^{1},\dots ,x^{k}\right]^{T}.}$

• Неперервний ланцюговий дріб

${\displaystyle \operatorname {E} _{1}(x)={\cfrac {{\rm {e}}^{-x}}{x+{\cfrac {1}{1+{\cfrac {1}{x+{\cfrac {2}{1+{\cfrac {2}{x+{\cfrac {3}{\dots }}}}}}}}}}}}}$.

• Наближення Баррі зі співавторами [16]

${\displaystyle \operatorname {E} _{1}(x)={\frac {{\rm {e}}^{-x}}{G+(1-G){\rm {e}}^{-{\frac {x}{1-G}}}}}\ln \left[1+{\frac {G}{x}}-{\frac {1-G}{(h+bx)^{2}}}\right]}$,

де

${\displaystyle h={\frac {1}{1+x{\sqrt {x}}}}+{\frac {h_{\infty }q}{1+q}}}$,

${\displaystyle q={\frac {20}{47}}x^{\sqrt {\frac {31}{26}}}}$,

${\displaystyle h_{\infty }={\frac {(1-G)\left(G^{2}-6G+12\right)}{3G(2-G)^{2}b}}}$,

${\displaystyle b={\sqrt {\frac {2(1-G)}{G(2-G)}}}}$,

${\displaystyle G={\rm {e}}^{-\gamma }}$,

${\displaystyle \gamma }$ — стала Ейлера–Маскероні.