Подільність
Подільність — властивість натуральних та цілих чисел. Число ділиться на , (відповідно, число є дільником якщо частка — ціле число
Будь-яке натуральне число ділиться на одиницю і на себе. Якщо число не має інших дільників, то таке число називається простим, в іншому разі — складеним.
Властивості простих чисел і питання подільності займали думки науковців принаймні з часів Піфагора, і досі не вичерпали себе. Завдяки розвитку криптографії і розповсюдженню заснованих на теорії чисел алгоритмів, пов'язані з перевіркою на простоту і факторизацією дослідження перебувають на передовому краю математики.
Історія
Питання подільності натуральних чисел розглядалися уже в античні часи. Евкліду належить один з найвідоміших результатів математики, твердження, що не існує найбільшого простого числа, тобто множина простих чисел — нескінченна. Він також навів найперший в історії алгоритм, а саме алгоритм Евкліда знаходження найбільшого спільного дільника двох натуральних чисел. Цікаво відзначити, що це — не тільки найдавніший, а й один з найефективніших алгоритмів в математиці, який майже не був вдосконалений за більш ніж дві тисячі років, що минули по тому. Але набагато раніше за Евкліда, Піфагор і піфагорійці розробили теорію досконалих і дружніх чисел, які відігравали важливу роль у їх філософській системі.
Подільність чисел, загальніших ніж цілі, було ретельно досліджено у 19 ст., починаючи з роботи Гауса про властивості гаусових цілих чисел, комплексних чисел вигляду , де — це звичайні цілі числа, а — це уявна одиниця. Гаус відкрив аналог алгоритму Евкліда і в такий спосіб довів однозначність факторизації гаусових цілих чисел. Чимало із спроб доведення великої теореми Ферма спиралося на однозначність факторизації алгебраїчних цілих чисел вигляду
де — це примітивний корінь з одиниці степені , a — цілі числа. Однак виявилося, що у випадку загального такі числа поводяться набагато складніше, ніж звичайні цілі, зокрема, для них не виконується однозначність факторизації на прості множники. У роботах Куммера, Кронекера і Дедекінда з теорії подільності алгебраїчних цілих чисел з'явились фундаментальні для сучасної математики поняття теорії кілець, на яких, разом з введеним Галуа поняттям групи, ґрунтується сучасна абстрактна алгебра.
Пов'язані визначення
- Одиниця має рівно один дільник і не є ні простою, ні складеною.
- У кожного натурального числа, більшого за одиницю, є хоча б один простий дільник.
- Власним дільником числа називається всякий його дільник, відмінний від самого числа. У простих чисел існує лише один власний дільник — одиниця.
- Незалежно від подільності цілого числа на ціле число , число a завжди можна розділити на b із залишком, тобто представити у вигляді:
- де .
- У цьому співвідношенні число називається неповною часткою, а число r — остачею від ділення на . Як частка, так і остача визначаються однозначно.
- Число a ділиться без остачі на b тоді та лише тоді, коли залишок від ділення a на b дорівнює нулю.
- Всяке число, яке ділить як , так і , називається їх спільним дільником; максимальне з таких чисел називається найбільшим спільним дільником. У будь-якої пари цілих чисел є принаймні два загальних подільника: +1 та −1. Якщо інших спільних дільників немає, то ці числа називають взаємно простими числами.
- Два цілих числа і називають одноподільними на ціле число , якщо або і , і ділиться на , або ні , ні не діляться на нього.
Позначення
- означає, що ділиться на , або що число кратне числу .
- або означає, що ділить , або, що теж cаме: — дільник .
Властивості
- Зауваження: у всіх формулах цього розділу передбачається, що — цілі числа.
- Будь-яке ціле число є дільником нуля, при цьому чаcтка дорівнює нулю :
- Будь-яке ціле число ділиться на одиницю:
- На нуль ділиться лише нуль:
- ,
причому частка в цьому випадку не визначена.
- Одиниця ділиться націло лише на одиницю:
- Для будь-якого цілого числа знайдеться таке ціле число для якого
- Якщо та то Звідси ж випливає, що якщо і то
- Для того щоб необхідно і достатньо, щоб
- Якщо то
- Властивість подільності є відношенням не суворого порядку і, зокрема, воно:
- рефлексивне, тобто будь-яке ціле число ділиться само на себе:
- транзитивне, тобто якщо і то
- антисиметричне, тобто якщо і то або або
Приклади
- 7 є дільник 42 оскільки , тому ми можемо сказати, . Крім того, можна сказати, що 42 ділиться на 7, 7 ділить 42.
- Нетривіальними дільниками 6 є 2, −2, 3, й −3.
- Додатними дільниками 42 є 1, 2, 3, 6, 7, 14, 21, 42.
- , оскільки .
- Множиною всіх додатних дільників 60 є, , частково впорядкована множина, якій відповідає діаграма Гассе:
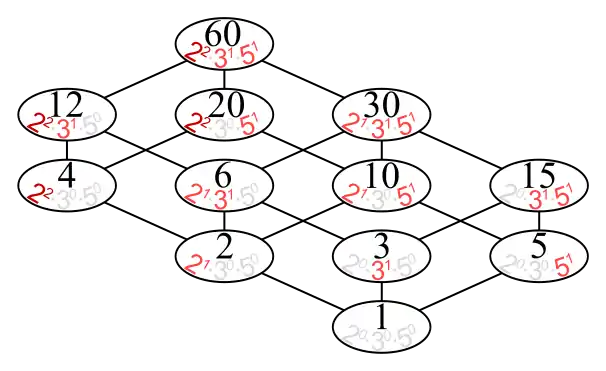
Кількість дільників
Число додатних дільників натурального числа зазвичай позначають , є мультиплікативною функцією, для неї є вірною асимптотична формула Діріхле:
в якій — стала Ейлера—Маскероні, а для Діріхле отримав значення Цей результат багаторазово поліпшувався, і останнім часом найкращий відомий результат (отримано у 2003 р. Хакслі). Однак, найменше значення , при якому ця формула залишиться вірною, невідоме (доведено, що воно не менше, ніж ).[1][2][3]
При цьому середній дільник великого числа n в середньому росте як , що було виявлено А. Карацубою.[4]. З комп'ютерних оцінок М. Корольова.
Узагальнення
Поняття подільності узагальнюється на довільні кільця, наприклад кільце многочленів.
Див. також
Примітки
- А. А. Бухштаб. Теорія чисел. — М. : Просвіта, 1966.
- Аналітична теорія чисел[недоступне посилання з жовтня 2019]
- Weisstein, Eric W. Dirichlet Divisor Problem(англ.) на сайті Wolfram MathWorld.
- В. І. Арнольд. Динаміка, статистика та проективна геометрія полів Галуа. — М. : МЦНМО, 2005. — С. 70.
Джерела
- Дрозд Ю. А. (1997). Теорія алгебричних чисел. Київ: РВЦ “Київський університет„. с. 82. ISBN 966-594-019-8. (укр.)
