Ін'єкція (математика)
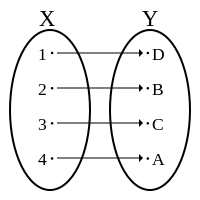
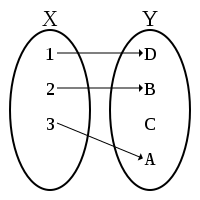
Ін'єкція (ін'єктивне відображення, ін'єктивна функція) — таке співвідношення між елементами двох множин, в якому двом різним елементам першої множини (області визначення) ніколи не співставляється один і той самий елемент другої множини (області значень).
Формально, відображення f: X → Y - ін'єктивне тоді й тільки тоді, коли для кожного y з Y, існує не більш як один (або жодного) x в X такий, що f(x) = y. Інакше: f є ін'єктивним, якщо для кожного x та x' з X, де f(x) = f(x'), виконується рівність x = x'.
Приклади
Нехай функція f: R → R визначена як f(x) = 2x + 1. Ця функція є ін'єктивною, тому що для будь-яких двох дійсних чисел x та x' , якщо 2x + 1 = 2x' + 1 , то обов'язково 2x = 2x' , таким чином x = x' .
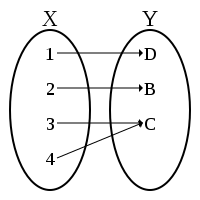
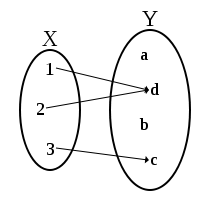
З іншого боку, функція g :R → R, визначена як g(x) = x2 не є ін'єктивною, тому що, наприклад, g(1) = 1 = g(−1).
|
|
|
|
|
|
Властивості
- Функція f : X → Y є ін'єктивною тоді й тільки тоді, якщо X є порожня множина, або існує функція g : Y → X така, що композиція функцій g o f є тотожним відображенням на X.
- За визначенням, функція є бієктивною, якщо вона є ін'єктивною та сюр'єктивною.
- Якщо g o f є ін'єктивною, то f також ін'єктивна.
- Якщо обидві f та g ін'єктивні, то g o f ін'єктивна.
- f : X → Y ін'єктивна тоді й тільки тоді, коли для будь-яких функцій g, h : W → X, де f o g = f o h, виконується рівність g = h.
- Якщо f : X → Y — ін'єктивна і A є підмножиною X, то f−1(f(A)) = A. Тобто, A може бути відновлений з образу функції f(A).
- Якщо f : X → Y є ін'єктивним, і A та B є підмножинами X, то f(A ∩ B) = f(A) ∩ f(B).
- Якщо f : X → Y — ін'єкція, то в Y щонайменше стільки ж елементів, скільки в X, в сенсі потужності множин.
- Якщо X та Y — скінченні з однаковою кількістю елементів, то f : X → Y ін'єктивне тоді й тільки тоді, коли f є сюр'єктивним.
Джерела
- Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — 4-е изд. — Москва : Наука, 1976. — 544 с. — ISBN 5-9221-0266-4.(рос.)