Алгоритм Метрополіса — Гастінгса

Алгоритм був названий на честь Ніколаса Метрополіса, який разом із Аріанною В. Розенблут, Маршаллом Розенблютом, Августою Х. Теллер та Едвардом Теллером написав у 1953 році статтю «Рівняння обчислень стану за допомогою швидких обчислювальних машин»[1].

Існує певна суперечка щодо авторства алгоритму. Метрополіс, який був знайомий з обчислювальними можливостями методу, ввів термін «Монте-Карло» у спільній із Станіславом Уламом статті. Він очолив групу у Теоретичному відділі, яка спроектувала та побудувала комп'ютер MANIAC I, який використовувався для експериментів в 1952 році. Однак, аж до 2003 року остаточної інформації про розробку алгоритму не було. Потім, незадовго до смерті, Маршалл Розенблут відвідав конференцію 2003 року в ЛАНЛ з нагоди 50-ї річниці публікації 1953 року. На цій конференції Розенблут описав алгоритм та його розробку у презентації під назвою «Генезіс алгоритму Монте-Карло для статистичної механіки»[2]. Подальші історичні роз'яснення робить Губернатіс у журнальній статті 2005 р.[3] Розенблут чітко дає зрозуміти, що він та його дружина Аріанна виконали цю роботу, і що Метрополіс не зіграв жодної ролі у розробці, крім надання комп'ютерного часу.

Алгоритм Метрополіса — Гастінгса може генерувати вибірки з будь-якого розподілу ймовірностей ${\displaystyle P(x)}$, за умови, що ми знаємо функцію ${\displaystyle f(x)}$, пропорційну густині ${\displaystyle P}$ , тому значення ${\displaystyle f(x)}$ можна розрахувати. Вимога, аби ${\displaystyle f(x)}$ була пропорційна густині ${\displaystyle P}$, а не точно їй рівна, робить алгоритм Метрополіса — Гастінгса особливо корисним, оскільки обчислення необхідного коефіцієнта нормалізації на практиці є часто надзвичайно складною задачею.

Алгоритм Метрополіса — Гастінгса працює шляхом генерації послідовності значень вибірки таким чином, що чим більше значень згенеровано, тим більше розподіл цих значень наближається до невідомого розподілу ${\displaystyle P(x)}$ . Ці значення вибірки генеруються ітеративно, причому розподіл наступної вибірки залежить лише від розподілу попередньої вібірки (таким чином, послідовність вибірки складається в ланцюжок Маркова). Потім, з певною ймовірністю, кандидат або приймається (у цьому випадку значення кандидата використовується в наступній ітерації), або відхиляється (у цьому випадку значення кандидата відкидається, а поточне значення використовується повторно в наступній ітерації) — ймовірність прийняття визначається порівнянням значень функції ${\displaystyle f(x)}$ поточного та кандидатського значення вибірки щодо бажаного розподілу ${\displaystyle P(x)}$ .

З метою ілюстрації, описаний алгоритм Метрополіса, є особливим випадком алгоритму Метрополіс – Гастінгс, де допоміжний розподіл є симетричним.

Метрополісів алгоритм (симетричний допоміжний розподіл)

Нехай ${\displaystyle f(x)}$ є функцією, пропорційною бажаному розподілу ймовірностей ${\displaystyle P(x)}$ (він же цільовий розподіл).

1. Ініціалізація: Виберіть довільну точку ${\displaystyle x_{t}}$ яка буде першим значенням у вибірці, та оберіть довільну густину ймовірності ${\displaystyle g(x\mid y)}$ (іноді позначається як ${\displaystyle Q(x\mid y)}$), що буде пропонувати кандидата наступного значення у вибірці ${\displaystyle x}$, на підставі попереднього значення вибірки — ${\displaystyle y}$ . Розподіл ${\displaystyle g}$ тут вважається симетричним; іншими словами, ${\displaystyle g}$ повинно задовольняти ${\displaystyle g(x\mid y)=g(y\mid x)}$ . Зазвичай, ${\displaystyle g(x\mid y)}$ має нормальний гауссовий розподіл центрований у точці ${\displaystyle y}$, тому точки ближчі до ${\displaystyle y}$ обираються частіше, перетворюючи послідовність зразків на випадкове блукання [lower-alpha 1] . Функція ${\displaystyle g}$ позначається як густина пропозиції або розподіл стрибків.
2. Для кожної ітерації t :
   • Згенеруйте наступне значення ${\displaystyle x'}$ з розподілу ${\displaystyle g(x'\mid x_{t})}$.
   • Обчисліть коефіцієнт прийняття ${\displaystyle \alpha =f(x')/f(x_{t})}$, який буде використаний для прийняття чи відхилення кандидата. Оскільки f пропорційна густині P, маємо: ${\displaystyle \alpha =f(x')/f(x_{t})=P(x')/P(x_{t})}$ .
   • Прийняти або відхилити :
     • Згенеруйте випадкове число із рівномірного розподілу ${\displaystyle u\in [0,1]}$ .
     • Якщо ${\displaystyle u\leq \alpha }$, приймаємо кандидата з розподілу ${\displaystyle g(x'\mid x_{t})}$, встановивши ${\displaystyle x_{t+1}=x'}$ ,
     • Якщо ${\displaystyle u>\alpha }$, відхиліть кандидата і встановіть ${\displaystyle x_{t+1}=x_{t}}$ (раніше обране перше значення у вибірці) натомість.

Цей алгоритм виконується шляхом рандомного переміщення по простору, іноді роблячи крок, а іноді залишаючись на місці. Зверніть увагу, що коефіцієнт прийняття ${\displaystyle \alpha }$ вказує, наскільки імовірна нова запропонована вибірка, враховуючи поточну вибірку, відповідно до розподілу ${\displaystyle P(x)}$ . Якщо ми робимо крок до точки, яка є більш вірогідною, ніж точка, у якій ми знаходимося зараз (тобто точка в області більшої густини ${\displaystyle P(x)}$ що відповідає ${\displaystyle \alpha >1\geq u}$), ми робимо крок. Однак, якщо ми намагаємось перейти до менш вірогідної точки, вірогідніше, ми залишаємося на місці, і чим менше значення густини ймовірності, тим більша ймовірність відхилити нову точку і залишитися на місці. Таким чином, ми будемо прагнути залишатися в області високих значень густини ${\displaystyle P(x)}$, приймаючи велику кількість зразків із цієї області, при цьому лише зрідка відвідуючи регіони із низькими значеннями густини. Інтуїтивно, саме тому цей алгоритм працює і повертає вибірки, які мають цільовий розподіл ${\displaystyle P(x)}$ .

Порівняно з таким алгоритмом як вибірка з відхиленням[4] , який безпосередньо генерує незалежні вибірки з розподілу, Метрополіс – Гастінгс та інші алгоритми MCMC мають ряд недоліків:

• Зразки корельовані. Хоча в довгостроковій перспективі вони мають густину ${\displaystyle P(x)}$, вибірки у наборі будуть корельований між собою, і набір не буде коректно відображати розподіл. Це означає, що якщо ми хочемо зразок із незалежними вибірками, нам доведеться викинути більшість вибірок і взяти лише кожну n-ту вибірку обраного значення n (як правило, обирається на закладі автокореляції між сусідніми зразками). Автокореляцію можна зменшити, збільшивши ширину стрибка (середній розмір стрибка, пов'язаний із дисперсією їх розподілу), але такий метод збільшить ймовірність відхилення запропонованого стрибка. Занадто великий або занадто малий розмір стрибків призведе до повільно-змішанного ланцюга Маркова, тобто, до сильно корельованого набору вибірок. Тому, аби отримати обґрунтоване значення параметру розподілу, потрібна дуже велика кількість вибірок.
• Хоча ланцюг Маркова з часом конвергує до бажаного розподілу, початкові вибірки можуть мати зовсім інший розподіл, особливо якщо початкова точка знаходиться в області із низьким значенням густини імовірності. В результаті, необхідний період прогорання[5] коли початкова кількість вибірок (наприклад, перші 1000 або близько того) викидаються.

З іншого боку, більшість простих методів відторгнення страждають від «проблеми розмірності», де ймовірність відхилення зростає в геометричній прогресії в залежності від кількості вимірів. Метрополіс — Гастінгс, поряд з іншими методами MCMC, так сильно не страждає від цієї проблеми, тому часто є єдиним доступним рішенням, коли вимірів розподілу, із якого генерується вибірка, багато. Як результат, методи MCMC часто використовуються для генерування вибірок з ієрархічних байєсівських моделей та інших високовимірних статистичних моделей, що використовуються сьогодні в багатьох дисциплінах.

У багатовимірних розподілах класичний алгоритм Метрополіса — Гастінгса, як описано вище, передбачає вибір нового багатовимірного значення вибірки. Коли розмірність велика, знайти відповідний розподіл стрибків може бути не легко, оскільки окремо узяті виміри поводяться дуже по-різному, а ширина стрибка (див. вище) повинна підходити для усіх вимірів одночасно, щоб уникайте надмірно повільного перемішування. Альтернативний підхід, який часто працює краще в таких ситуаціях, відомий як Семплування за Гіббсом, передбачає генерування нової вибірки для кожного виміру окремо, а не для всіх вимірів одночасно. Метод часто використовується, коли багатовимірний розподіл складається з набору окремих випадкових величин, в яких кожна змінна зумовлена лише невеликою кількістю інших змінних, як, наприклад, у більшості типових ієрархічних моделях. Потім окремі змінні обираються по черзі, причому кожна змінна обирається на закладі найсвіжіших значень усіх інших. Для вибору цих окремих вирірок можуть бути використані різні алгоритми, в залежності від форми багатовимірного розподілу: наприклад, — вибірка з відхиленням[4], алгоритм вибірки з відхиленням Метрополіса[6], простий одновимірний Метрополіс — Гастінгув крок, або зрізове семплування .

Метою алгоритму Метрополіс – Гастінгс є створення колекції станів відповідно до бажаного розподілу ${\displaystyle P(x)}$ . Для цього алгоритм використовує ланцюги Маркова, які асимптотично досягають унікального стаціонарного розподілу ${\displaystyle \pi (x)}$ такого, що ${\displaystyle \pi (x)=P(x)}$[7].

Процес Маркова однозначно визначається його перехідними ймовірностями ${\displaystyle P(x'\mid x)}$, ймовірність переходу з будь-якого даного стану ${\displaystyle x}$ до будь-якої іншої стану ${\displaystyle x'}$. Він має унікальний стаціонарний розподіл ${\displaystyle \pi (x)}$ коли виконуються наступні дві умови[7]:

1. Існування стаціонарного розподілу : повинен існувати стаціонарний розподіл ${\displaystyle \pi (x)}$ . Достатньою, але не необхідною умовою є детальний баланс, який вимагає аби кожен перехід ${\displaystyle x\to x'}$ був оборотним: для кожної пари станів ${\displaystyle x,x'}$, ймовірність перебування в стані ${\displaystyle x}$ і перехід до стану ${\displaystyle x'}$ повинен дорівнювати ймовірності перебування в стані ${\displaystyle x'}$ і переходу до стану ${\displaystyle x}$, ${\displaystyle \pi (x)P(x'\mid x)=\pi (x')P(x\mid x')}$ .
2. Унікальність стаціонарного розподілу : стаціонарний розподіл ${\displaystyle \pi (x)}$ має бути унікальним. Це гарантується ергодичністю процесу Маркова, який вимагає, щоб кожен стан (1) був аперіодичним - система не повертається до того ж стану на визначених проміжках; і (2) був позитивно рекурентним - очікувана кількість кроків для повернення до того самого стану є кінцевою.

Алгоритм Метрополіс — Гастінгс передбачає розробку процесу Маркова (шляхом побудови ймовірностей переходу), який відповідає двом вищезазначеним умовам, таким чином, що його стаціонарний розподіл ${\displaystyle \pi (x)}$ є ${\displaystyle P(x)}$. Виведення алгоритму починається з умови детального балансу:

${\displaystyle P(x'\mid x)P(x)=P(x\mid x')P(x'),}$

який переписується як

${\displaystyle {\frac {P(x'\mid x)}{P(x\mid x')}}={\frac {P(x')}{P(x)}}.}$

Підхід полягає у розділенні переходу на два підкроки; пропозиція та прийняття-відхилення. Розподіл пропозиції ${\displaystyle g(x'\mid x)}$ - це умовна ймовірність пропозиції стану ${\displaystyle x'}$ за умови стану ${\displaystyle x}$. Розподіл прийняття ${\displaystyle A(x',x)}$ це ймовірність прийняти запропонованого стану ${\displaystyle x'}$ . Імовірність переходу можна записати як добуток:

${\displaystyle P(x'\mid x)=g(x'\mid x)A(x',x).}$

Вставивши це відношення в попереднє рівняння, маємо

${\displaystyle {\frac {A(x',x)}{A(x,x')}}={\frac {P(x')}{P(x)}}{\frac {g(x\mid x')}{g(x'\mid x)}}.}$

Наступним кроком є вибір коефіцієнта прийняття який відповідає наведеній вище умові. Одним із поширених варіантів є вибір Метрополіса:

${\displaystyle A(x',x)=\min \left(1,{\frac {P(x')}{P(x)}}{\frac {g(x\mid x')}{g(x'\mid x)}}\right).}$

Для цього коефіцієнта прийняття Метрополіса ${\displaystyle A}$, це або ${\displaystyle A(x',x)=1}$ або ${\displaystyle A(x,x')=1}$ і, в обох випадках, умова виконана.

Таким чином, алгоритм Метрополіс – Гастінгс полягає у наступному:

1. Ініціалізація
   1. Виберіть початковий стан ${\displaystyle x_{0}}$ .
   2. Встановіть ${\displaystyle t=0}$ .
2. Ітерація
   1. Згенеруйте випадковий стан ${\displaystyle x'}$ відповідно до ${\displaystyle g(x'\mid x_{t})}$ .
   2. Обчисліть ймовірність прийняття ${\displaystyle A(x',x_{t})=\min \left(1,{\frac {P(x')}{P(x_{t})}}{\frac {g(x_{t}\mid x')}{g(x'\mid x_{t})}}\right)}$ .
   3. Прийняти або відхилити :
      1. генерувати випадкове число із рівномірного розподілу ${\displaystyle u\in [0,1]}$ ;
      2. якщо ${\displaystyle u\leq A(x',x_{t})}$, прийміть новий стан і встановіть ${\displaystyle x_{t+1}=x'}$ ;
      3. якщо ${\displaystyle u>A(x',x_{t})}$, відхиліть новий стан ${\displaystyle x'}$, натомість оберіть старий стан ${\displaystyle x_{t+1}=x_{t}}$ .
   4. Приріст: збільшіть на одиничку ${\displaystyle t=t+1}$ .

За умови виконання заданих умов здійснюється емпіричний розподіл збережених станів ${\displaystyle x_{0},\ldots ,x_{T}}$ наближуватиметься розподілу ${\displaystyle P(x)}$ . Кількість ітерацій ( ${\displaystyle T}$ ), яка необхідна для ефективної оцінки ${\displaystyle P(x)}$ залежить від кількості факторів, включаючи взаємозв'язок між ${\displaystyle P(x)}$ і допоміжним розподілом, та бажаною точністю оцінки. [8] Для дискретних розподілів стану, вони повинні бути впорядкованою автокореляцією процесу Маркова[9].

Важливо зауважити, що в загальному невідомо, який розподіл ${\displaystyle g(x'\mid x)}$ слід використовувати або скільки необхідно ітерацій для правильної оцінки; це вільні параметри методу, які повинні обиратися відповідно до конкретної проблеми.

${\displaystyle a_{1}={\frac {P(x')}{P(x_{t})}}}$

де

Ланцюг Маркова починається з довільного початкового значення ${\displaystyle x_{0}}$, і алгоритм виконує багато ітерацій (приблизно 1000), поки цей початковий стан не буде «забутий». Ці значення відкидаються як прогорівші.Ті значення ${\displaystyle x}$, що залишились, представляють сабою вирірку з розподілу ${\displaystyle P(x)}$ .

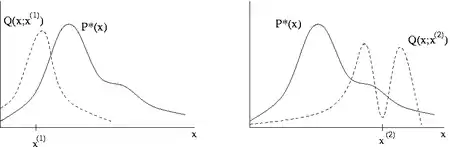
Припустимо, що останнє значення вибірки — ${\displaystyle x_{t}}$. За алгоритмом Метрополіса — Гастінгса, ми далі обираємо новий допоміжний стан ${\displaystyle x'}$ з густиною імовірності ${\displaystyle g(x'\mid x_{t})}$ і обчислюємо значення

${\displaystyle a=a_{1}a_{2},}$

${\displaystyle a_{2}={\frac {g(x_{t}\mid x')}{g(x'\mid x_{t})}}}$

- це ймовірне (наприклад, байєсівське апостеріорне) співвідношення між запропонованою вибіркою ${\displaystyle x'}$ і попередньою ${\displaystyle x_{t}}$, а

- це відношення допоміжної густини у двох напрямках (від ${\displaystyle x_{t}}$ до ${\displaystyle x'}$, і навпаки). Воно дорівнює 1, якщо допоміжна густина симетрична. Потім новий стан ${\displaystyle x_{t+1}}$ обирається згідно з наступними правилами.

Якщо ${\displaystyle a\geq 1{:}}$

${\displaystyle x_{t+1}=x',}$

ще:

${\displaystyle x_{t+1}={\begin{cases}x'&{\text{with probability }}a,\\x_{t}&{\text{with probability }}1-a.\end{cases}}}$

Алгоритм працює краще, якщо допоміжна густина відповідає формі цільового розподілу ${\displaystyle P(x)}$, з якого безпосереднє просте пряме семплування є майже неможливим, тобто ${\displaystyle g(x'\mid x_{t})\approx P(x')}$. Якщо використовується допоміжна густина Гауса ${\displaystyle g}$, параметр дисперсії ${\displaystyle \sigma ^{2}}$ повинен бути налаштований під час прогорання. Зазвичай це робиться шляхом обчислення коефіцієнта приймання, який є часткою пропонованих значень, які приймаються серед останніх ${\displaystyle N}$ значень. Бажаний коефіцієнт прийняття залежить від цільового розподілу, проте теоретично було показано, що ідеальний коефіцієнт прийняття для одновимірного гауссового розподілу становить близько 50%, зменшуючись до приблизно 23% для ${\displaystyle N}$-вимірного цільового Гаусовського розподілу[10].

Якщо ${\displaystyle \sigma ^{2}}$ занадто мала, ланцюг буде повільно змішуватися (тобто коефіцієнт прийняття буде високим, але обрані значення будуть повільно рухатися по простору, і ланцюг буде лише повільно конвергувати до ${\displaystyle P(x)}$). З іншого боку, якщо ${\displaystyle \sigma ^{2}}$ занадто велика, коефіцієнт прийняття буде дуже низьким, оскільки значення, ймовірно, будуть обиратися із регіонів із набагато меншою густиною ймовірності, тому ${\displaystyle a_{1}}$ буде дуже маленьким, і знову ланцюг буде сходитися дуже повільно. Зазвичай налаштовують розподіл пропозицій таким чином, щоб алгоритми приймали близько 30 % усіх вибірок — відповідно до теоретичних оцінок, згаданих у попередньому параграфі.

Результат трьох ланцюжків Маркова, на 3D функції Розенброка з використанням алгоритму Метрополіса — Гастінгса. Алгоритм бере вибірки з регіонів, де апостеріорна ймовірність велика, і ланцюги починають змішуватися в цих регіонах. Приблизне положення максимуму підсвічено на малюнку. Червоні точки — це ті, які залишаються після процесу прогорання. Більш ранні були відкинуті.

• Детальний баланс
• Генетичні алгоритми
• Семплування за Гіббсом
• Методи частинок середнього поля
• Послідовний Монте-Карло
• Імітований відпал

1. In the original paper however, ${\displaystyle g(x\mid y)}$ was actually the Boltzmann distribution, as it was applied to physical systems in the context of statistical mechanics