Антипризма

Антипри́зма (англ. antiprism) — призматоїд, у якого дві паралельні грані (основи) — рівні між собою многокутники з n вершинами (n-кутники), а решта 2n граней (бокові грані) — трикутники, що поперемінно спрямовані вершинами до однієї і та до іншої основ. Якщо основами антипризми є правильні n-кутники а у гранях — рівносторонні трикутники то така антипризма є правильною і належить до напівправильних многогранників.

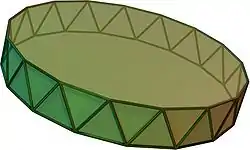
Антипризма на основі правильного 17-кутника

Правильна антипризма з п'ятикутною основою

Антипризми іменують за числом вершин многокутника, що лежить в основах: трикутна антипризма (для випадку правильної — октаедр), квадратна антипризма (для випадку правильної — антикуб), п'ятикутна антипризма і т. д.

Октаедр є правильною антипризмою з трикутними основами. Ікосаедр може бути складений з п'ятикутної правильної антипризми і двох правильних п'ятикутних пірамід.

Антипризма у декартовій системі координат

Декартові координати вершин антипризми з правильним n-кутником в основі й правильними трикутниками у бокових гранях

\left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)

де k цілі числа від 0 до 2n−1;

h={\sqrt {\frac {\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}}{2}}}.

Об'єм і площа поверхні

Нехай a — довжина ребра правильної антипризми. Тоді її об'єм обчислюється за формулою:

V={\frac {n{\sqrt {4\cos ^{2}{\frac {\pi }{2n}}-1}}\sin {\frac {3\pi }{2n}}}{12\sin ^{2}{\frac {\pi }{n}}}}\;a^{3},

а площа поверхні за формулою:

S={\frac {n}{2}}(\cot {\frac {\pi }{n}}+{\sqrt {3}})a^{2}.

Див. також

Призма

Джерела

Гордєєва Є. П. Ч. 1 // Нарисна геометрія. Багатогранники (правильні, неправильні та зірчасті) : навч. посіб. для студ. вищ. навч. закл / Є. П. Гордєєва, В. Л. Величко. — Луцьк : ЛДТУ, 2007. — 191 с. — ISBN 978-966-7667-70-2.
Ашкинузе В. Г. О числе полуправильных многогранников // Математическое просвещение. Вторая серия. — 1957. — Вип. 1. — С. 107-118.
М. Веннінджер. Модели многогранников. — Мир, 1974.
Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова, А. И. Маркушевича, Хинчин, А. Я. Хинчина. — М. : Государственное издательство физико-математической литературы, 1963. — С. 382-447.

Посилання

Weisstein, Eric W. Antiprism(англ.) на сайті Wolfram MathWorld.
George W. Hart Prism and Antiprism (англ.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.