Призматоїд
Призмато́їд (від грец. prísma, родовий відмінок грец. prísmatos — призма та грец. éidos — вид) — многогранник, дві грані якого (основи) є многокутниками з довільною кількістю сторін, що лежать у паралельних площинах, а решта — трикутники або трапеції, причому у трикутників одна сторона, а у трапецій обидві основи є сторонами основ призматоїда[1].
Об'єм призматоїда
де h — віддаль між основами призматоїда,
- і — площі основ,
- — площа перерізу, рівновіддаленого від обох основ.
Сімейство призматоїдів
Сімейство призматоїдів включає наступні многогранники, як часткові випадки:
- Піраміда — призматоїд, у якого одна з основ є точкою.
- Клин — призматоїд, у якого одна з основ є відрізком прямої.
- Призма — призматоїд, у якого основи однакові, а сторони є прямокутниками або паралелограмами (окремі випадки — паралелепіпеди).
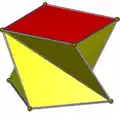
- Антипризма — призматоїд, у якого основи однакові многокутники, а сторони є правильними трикутниками.
- Купол — призматоїд, у якого одна з основ є многокутником із удвічі більшою кількістю сторін, а бокові грані є почергово прямокутниками і трикутниками.
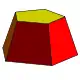
- Зрізана піраміда — призматоїд, у якого основи є різні за розміром та мають однакову кількість сторін, а бічні грані є трапеціями.
| Піраміди | Клини | Призми | Антипризми | Куполи | Зрізані піраміди | ||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 | ||
Примітки
- William F. Kern, James R Bland Solid Mensuration with proofs, 1938, p.75
Джерела
- Фольта О. В., Антонович С. А., Юрковський П. В. Нарисна геометрія. — Л.: Світ, 1994. — 303 с. — ISBN 5-7773-0115-0
- Теоретичні положення та методичні рекомендації за темою «Конструювання деяких поверхонь та перетин їх прямою» Для самостійної роботи студентів машинобудівних спеціальностей /Укладачі. Н. О. Федоренко та ін. — Харків: НТУ «ХПІ», 2003 — 39 с.
Посилання
- Призматоїд // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 160. — ISBN 978-966-7407-83-4.
- «Призматоїд» в УРЕ
- Weisstein, Eric W. Prismatoid на MathWorld.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
