Група кубика Рубіка

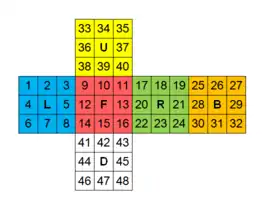
У 3×3×3 кубика 6 граней по 9 етикеток, але центральні етикетки граней при будь-яких рухах залишаються на своїх місцях.

Позначимо центри граней літерами ${\displaystyle \{L,F,R,B,U,D\}}$ (див. малюнок), а інші етикетки — числами від 1 до 48.

Тепер поворотам відповідних граней на 90° за годинниковою стрілкою ми можемо зіставити елементи симетричної групи ${\displaystyle S_{48}}$ етикеток кубика Рубіка, які не є центрами граней:

${\displaystyle L=(1,3,8,6)(2,5,7,4)(33,9,41,32)(36,12,44,29)(38,14,46,27)}$

${\displaystyle F=(9,11,16,14)(10,13,15,12)(38,17,43,8)(39,20,42,5)(40,22,41,3)}$

${\displaystyle R=(17,19,24,22)(18,21,23,20)(48,16,40,25)(45,13,37,28)(43,11,35,30)}$

${\displaystyle B=(25,27,32,30)(26,29,31,28)(19,33,6,48)(21,34,4,47)(24,35,1,46)}$

${\displaystyle U=(33,35,40,38)(34,37,39,36)(25,17,9,1)(26,18,10,2)(27,19,11,3)}$

${\displaystyle D=(41,43,48,46)(42,45,47,44)(6,14,22,30)(7,15,23,31)(8,16,24,32)}$

Тоді група кубика Рубіка ${\displaystyle G}$ визначається як підгрупа ${\displaystyle S_{48}}$, породжена поворотами шести граней на 90°[1]:

${\displaystyle G=\langle L,F,R,B,U,D\rangle }$

Порядок групи ${\displaystyle G}$ дорівнює[1][2][3][4][5]

${\displaystyle |G|={\dfrac {8!\cdot 12!\cdot 3^{8-1}\cdot 2^{12-1}}{2}}=43\ 252\ 003\ 274\ 489\ 856\ 000=2^{27}\cdot 3^{14}\cdot 5^{3}\cdot 7^{2}\cdot 11}$

Нехай ${\displaystyle K_{f}}$ — граф Келі групи ${\displaystyle G}$ з 18 утворюючими, які відповідають 18 ходам метрики FTM.

Кожна з ${\displaystyle 4{,}32\cdot 10^{19}}$ конфігурацій може бути вирішена не більше ніж за 20 ходів FTM. Іншими словами, ексцентриситет вершини графу ${\displaystyle K_{f}}$, яка відповідає «зібраному» стану головоломки, дорівнює 20[6].

Діаметр графу ${\displaystyle K_{f}}$ також дорівнює 20[7].

Найбільший порядок елемента в ${\displaystyle G}$ дорівнює 1260. Наприклад, послідовність ходів ${\displaystyle (R\ U^{2}\ D^{\prime }\ B\ D^{\prime })}$ необхідно повторити 1260 разів[8], перш ніж кубик Рубіка повернеться до початкового стану[9].

${\displaystyle G}$ не є абелевою групою, оскільки, наприклад, ${\displaystyle FR\neq RF}$. Іншими словами, не всі пари поворотів комутують[10].

Етикетки, що знаходяться в центрах граней кубика Рубіка, не переміщаються, але повертаються. На звичайному кубику Рубіка орієнтація центрів граней невидима.

Група всіх рухів кубика Рубіка з видимими орієнтаціями центрів граней називається супергрупою кубика Рубика. Вона в ${\displaystyle {\dfrac {4^{6}}{2}}=2048}$ разів більше групи ${\displaystyle G}$[4].

На графі Келі ${\displaystyle K_{q}}$ групи ${\displaystyle G}$ з 12 утворюючими, які відповідають ходам метрики QTM, існує гамільтонів цикл. Знайдений цикл використовує повороти лише 5 з 6 граней[12][13].

Існує відповідна гіпотеза Ласло Ловаса для довільного графу Келі.

• Гамільтонів граф
• Граф Келі
• Математика кубика Рубіка
• Нормальна підгрупа
• Перестановка
• Теорія груп

• Joyner, David (2002). Adventures in group theory: Rubik's Cube, Merlin's machine, and Other Mathematical Toys. Baltimore: Johns Hopkins University Press. ISBN 0-8018-6947-1.

• W. D. Joyner. Lecture notes on the mathematics of the Rubik's cube (англ.). Архів оригіналу за 5 вересня 2013. Процитовано 22 липня 2013.