Двогранний граф

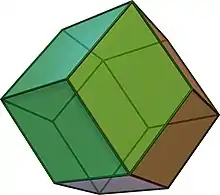
Кожен повний дводольний граф ${\displaystyle K_{a,b}}$ є ${\displaystyle (b,a)}$-двогранним[3]. Ромбододекаедр є ще одним прикладом; він є (3,4)-двогранним графом[4] .

${\displaystyle (x,y)}$-двогранний граф ${\displaystyle G=(U,V,E)}$ має задовольняти рівняння ${\displaystyle x|U|=y|V|}$. Це випливає з простого аргументу подвійного підрахунку: кількість кінців ребер з ${\displaystyle U}$ дорівнює ${\displaystyle x|U|}$, кількість кінців ребер в ${\displaystyle V}$ дорівнює ${\displaystyle y|V|}$, і кожне ребро додає однакову кількість в обидва числа.

Кожен регулярний дводольний граф також є двогранним. Кожен реберно-транзитивний граф (забороняються графи з ізольованими вершинами), який не є також вершинно-транзитивним, повинен бути двогранним[3]. Зокрема, кожен реберно-транзитивний граф є або регулярним, або бірегулярним (двогранним).

Графи Леві геометричних конфігурацій є двогранними; двогранний граф — це граф Леві (абстрактної) конфігурації тоді й тільки тоді, коли його обхват становить не менше шести[5].