Джиріх (математика)

Мозаїки «джиріх»[1] — це набір із п'яти плиток, що використовувалися для створення орнаменту для прикрашання будівель в ісламській архітектурі. Плитки використовувалися приблизно з XII століття і орнаменти істотно покращилися до моменту побудови усипальниці Дарб-і Імам у місті Ісфаган в Ірані (побудована в 1453).

Плитки «джиріх»
Візерунок з плиток «джиріх»
Візерунок з плиток «джиріх» (плитки й візерунок окремо)

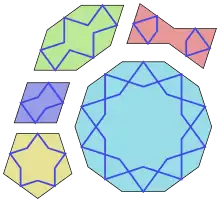
П'ять плиток мозаїки включають:

  • правильний десятикутник з внутрішніми кутами 144°;
  • подовжений (неправильний опуклий) шестикутник зі внутрішніми кутами 72°, 144°, 144°, 72°, 144°, 144°;
  • краватка-метелик (неопуклий шестикутник) зі внутрішніми кутами 72°, 72°, 216°, 72°, 72°, 216°;
  • ромб зі внутрішніми кутами 72°, 108°, 72°, 108°;
  • правильний п'ятикутник зі внутрішніми кутами 108°.

Всі сторони цих плиток мають однакову довжину, а всі кути кратні 36° (π/5 рад). Чотири плитки (крім п'ятикутника) мають двосторонню (дзеркальну) симетрію відносно двох перпендикулярних осей. Деякі плитки мають додаткові симетрії. Зокрема, десятикутник має десятикратну обертову симетрію (обертання на 36°), а п'ятикутник має п'ятикратну обертову симетрію (обертання на 72°).

Власне, джиріх — це лінії (орнаменту), яким декоровані плитки. Плитки використовувалися для створення орнаменту (джиріх). Мовою фарсі слово گره означає «вузол»[2]. У більшості випадків видно тільки джиріх (та інші прикраси у вигляді квітів), але не межі самих плиток. Джиріх є ламаними відрізками, що перетинають межі плиток по центру під кутом 54° (3π/10) до ребра. Дві перехресні лінії джиріх перетинають кожне ребро плитки. Більшість плиток мають єдиний орнамент всередині, відповідний симетрії плитки. Однак десятикутник має два можливих орнаменти джиріх, один з яких має тільки п'ятикратну, а не десятикратну симетрію.

Математика плиток джиріх

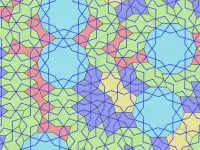
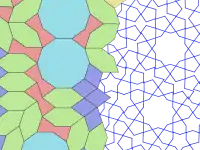
У 2007 році фізики Пітер Дж. Лу і Пол Стейнхардт висловили припущення, що мозаїка джиріх має властивості, які можна порівняти з властивостями самоподібних фрактальних квазікристалічних мозаїк, таких як мозаїки Пенроуза, але вік джиріх налічує п'ять століть[3].

Це відкриття підтверджено як аналізом наявних орнаментів, так і вивченням перських сувоїв XV століття. Однак немає жодних натяків, чи знали архітектори що-небудь про залучену математику. Переважає думка, що такі візерунки створювали, малюючи звивисті контури за допомогою лінійки і циркуля. Досліджують візерунки, знайдені в сувоях, таких як сувій Топкапи, довжиною 29,5 м. Знайдений у палаці Топкапи в Стамбулі, адміністративному центрі Османської імперії, і датований, як вважають, кінцем XV століття, сувій містить послідовність двомірних і тривимірних геометричних візерунків. На сувої немає тексту, але є сітка і позначені кольором симетрії і різні тривимірні проєкції. Малюнки в сувої могли бути зразками орнаментів для художників, які виготовляли плитки, а форми плиток джиріх визначали, яким чином їх можна скомбінувати для отримання орнаменту. Таким чином робітники могли робити дуже складні орнаменти без залучення математики й без розуміння принципів, на яких вони ґрунтуються[4].

Створення повторюваних орнаментів з обмеженого числа геометричних фігур, доступних робітникам того часу, схоже на практику сучасніших готичних європейських майстрів. Художники обох стилів, ґрунтуючись на наявних геометричних фігурах, зосереджувалися на створенні якомога відмінніших орнаментів. Це вимагало зовсім іншої кваліфікації і досвіду, ніж у математиків[4].

Приклади
  • Приклади орнаментів
  • Складні джиріх-орнаменти з 16-, 10- і 8-кутними зірками в різному масштабі на стелі могили Хафеза в Ширазі, 1935
  • Вікно в апартаментах кронпринца в палаці Топкапи, Стамбул, Туреччина, з 6-кутними зірками. Оточення зірки має вигляд квітки.
  • Внутрішній вигляд арки в Зеленій мечеті в Бурсі, Туреччина (1424), з 10-кутними зірками і п'ятикутниками

Див. також

Примітки
  1. «Джиріх» у перекладі з фарсі — «вузли». В цій статті розглянуто лише математичні аспекти орнаментів, про сам орнамент читайте статтю «Джиріх».
  2. Prange, 2009, с. 24–31.
  3. Lu, Steinhardt, 2007, с. 1106–1110.
  4. Necipoglu, 1995.

Література

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.