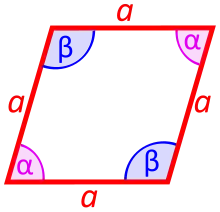
Ромб
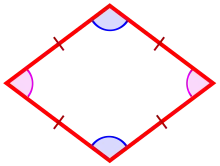
Ромб (грец. ρομβος) — це паралелограм, у якого всі сторони рівні.
| Ромб | |
|---|---|
 Два ромби | |
| Вид | чотирикутник, паралелограм, дельтоїд |
| Ребра і вершини | 4 |
| Символ Шлефлі | { } + { } |
| Діаграма Коксетера |
|
| Група симетрії | діедральна (D2), [2], (*22), порядок 4 |
| Площа | (половина добутку діагоналей) |
| Дуальний багатокутник | прямокутник |
| Властивості | опуклий, ізотоксальний |
Ромб, сторони якого утворюють прямий кут, називають квадратом.
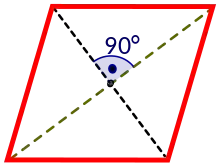
Діагоналі ромба перетинаються під прямим кутом. Діагоналі ромба є бісектрисами його кутів.
Етимологія
Слово «ромб» походить від грец. ῥόμβος (ромбос), що означає щось, що обертається[1], утворене своєю чергою від дієслова ῥέμβω (рембо), що означає «обертаюся довкола»[2]. Слово використовувалося Евклідом і Архімедом, які використовували термін «об'ємний суцільний ромб» для двох круглих конусів зі спільною основою[3].
Та плоска фігура, яку ми сьогодні називаємо ромбом, є поздовжнім перетином того суцільного ромба, що проходить крізь вершини кожного з двох конусів.
Ознаки ромба
Паралелограм ABCD буде ромбом, якщо виконується хоча б одна з таких умов:
- Дві його суміжні сторони рівні (звідси випливає, що всі сторони рівні): АВ = ВС = СD = AD
- Його діагоналі перетинаються під прямим кутом: AC┴BD
- Одна із діагоналей (бісектриса) ділить кути навпіл:
∠BAC = ∠CAD або ∠BDA = ∠BDC - Якщо всі висоти рівні: BN = DL = BM = DK
- Якщо діагоналі ділять паралелограм на чотири рівні прямокутні трикутники:
Δ ABO = Δ BCO = Δ CDO = Δ ADO - Якщо в паралелограм можна вписати коло.
Властивості ромба
Кожен ромб має дві діагоналі, що з'єднують пари протилежних вершин, і має дві пари паралельних сторін. Використовуючи правила конгруентних трикутників, можна довести, що ромб є симетричним відносно кожної з його діагоналей. Звідси випливає, що ромб має такі властивості:
- Це паралелограм, діагоналі якого розділяють внутрішній кут.
- Протилежні кути ромба рівні.
- Діагоналі ромба перетинаються під прямим кутом, точка перетину є серединою кожної діагоналі.
- Діагоналі ромба є бісектрисами кутів, з яких вони проведені.
- Сторони ромба попарно паралельні.
- Точка перетину діагоналей називається центром симетрії ромба.
- В будь-який ромб можна вписати коло.
- Центром кола, вписаного в ромб, є точка перетину його діагоналей.
- Сума квадратів діагоналей дорівнює квадрату сторони, помноженому на чотири: AC2 + BD2 = 4AB2
Однією з основних властивостей є те, що ромб - це паралелограм, внаслідок чого ромб має усі ті властивості, що й паралелограм. Наприклад,
- протилежні сторони паралельні;
- прилеглі кути є суміжними;
- дві діагоналі поділяють одна одну навпіл;
- будь-яка пряма, що проходить через центр, поділяє площу навпіл;
- сума квадратів сторін дорівнює сумі квадратів діагоналей (правило паралелограма).
Отож, якщо позначити сторону як a, а діагоналі як d1 і d2, то для кожного ромба
Не кожен паралелограм є ромбом, але кожен паралелограм, у якого діагоналі є перпендикулярними, є ромбом. В загальному випадку будь-який чотирикутник з перпендикулярними діагоналями, одна з яких є лінією симетрії, - це дельтоїд.
Сторона ромба
Формули визначення довжини сторони ромба
1. Формула сторони ромба через площу і висоту:
2. Формула сторони ромба через площу і синус кута:
3. Формула сторони ромба через площу і радіус вписаного кола:
4. Формула сторони ромба через дві діагоналі:
5. Формула сторони ромба через діагональ і косинус гострого кута (cos α) або косинус тупого кута (cos β):
6. Формула сторони ромба через більшу діагональ і половинний кут:
7. Формула сторони ромба через малу діагональ і половинний кут:
8. Формула сторони ромба через периметр:
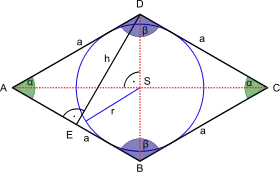
Діагоналі ромба
Діагональ ромба — це відрізок, що з'єднує дві вершини протилежних кутів ромба.
Ромб має дві діагоналі — більшу d1, та меншу — d2
Формули визначення довжини діагоналі ромба
1. Формули більшої діагоналі ромба через сторону і косинус гострого кута (cosα) або косинус тупого кута (cosβ)
2. Формули меншої діагоналі ромба через сторону і косинус гострого кута (cosα) або косинус тупого кута (cosβ)
3. Формули більшої діагоналі ромба через сторону і половинний кут:
4. Формули меншої діагоналі ромба через сторону і половинний кут:
5. Формули діагоналей ромба через сторону і другу діагональ:
6. Формули діагоналей через тангенс гострого tgα або тупого tgβ кута і другу діагональ:
7. Формули діагоналей через площу і другу діагональ:
8. Формули діагоналей через синус половинного кута і радіус вписаного кола:
Периметр ромба
Периметром ромба називається сума довжин всіх сторін ромба.
Формула периметра ромба через сторону ромба:
Площа ромба
Площа ромба — це простір, обмежений сторонами ромба, тобто в межах периметра ромба.
Формули визначення площі ромба
1. Формула площі ромба через сторону і висоту:
2. Формула площі ромба через сторону і синус будь-якого кута:
3. Формула площі ромба через сторону і радіус:
4. Формула площі ромба через дві діагоналі:
5. Формула площі ромба через синус кута і радіус вписаного кола:
6. Формули площі через більшу діагональ і тангенс гострого кута (tgα) або малу діагональ і тангенс тупого кута (tgβ):
Коло, вписане у ромб

Колом, вписаним у ромб, називається коло, що дотикається до всіх сторін ромба та має центр на перетині діагоналей ромба.
Формули визначення радіуса кола, вписаного в ромб
1. Формула радіуса кола, вписаного в ромб, через висоту ромба:
2. Формула радіуса кола, вписаного в ромб, через площу та сторону ромба:
3. Формула радіуса кола, вписаного в ромб, через площу та синус кута:
4. Формули радіуса кола, вписаного в ромб, через сторону і синус будь-якого кута:
5. Формули радіуса кола, вписаного в ромб, через діагональ та синус кута:
6. Формула радіуса кола, вписаного в ромб, через дві діагоналі:
7. Формула радіуса кола, вписаного в ромб, через дві діагоналі та сторону:
Рівняння
Сторони ромба, центр якого суміщено з центром координат із діагоналями, що розташовані на осях, будуть складатися із точок (x, y), що задовільняють рівняння
Вершини знаходитимуться в точках і Це є особливим випадком супереліпса із експонентою 1.
Див. також
Примітки
- ῥόμβος, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ρέμβω, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- The Origin of Rhombus. Архів оригіналу за 2 квітня 2015. Процитовано 23 лютого 2018.
Посилання
- Ромб // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 174. — ISBN 978-966-7407-83-4.
- Ромб. Формули, ознаки та властивості ромба
