Ефект Зеемана
Ефе́кт Зе́емана — явище розщеплення вироджених квантово-механічних станів та ліній оптичних спектрів у зовнішньому магнітному полі.
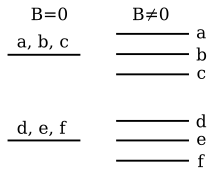


Ефект Зеемана названий на честь нідерландського фізика Пітера Зеемана, що отримав за його відкриття Нобелівську премію з фізики 1902 року.
Зееман виявив, що лінії в лінійчатих оптичних спектрах розщеплюються на компоненти в магнітному полі. Чим більша напруженість магнітного поля, тим сильніше розщеплення. Квантова механіка пояснила явище розщеплення зняттям виродження електронних термів, тож зняття виродження стали називати ефектом Зеемана.
Фізична природа
Завдяки ізотропності простору енергетичні рівні квантовомеханічної системи зазвичай не залежать від магнітного квантового числа (на мові фізиків незалежність енергії від квантового числа називають виродженням). Однак у магнітному полі ізотропність зникає. Навіть у площині, перпендикулярній до напрямку поля, рух проти годинникової стрілки відрізняється від руху за годинниковою стрілкою, а отже, якщо фізична система, наприклад, атом чи молекула мають орбітальний момент, то в прикладеному магнітному полі їхня енергія змінюється залежно від напрямку обертання в системі.
З погляду класичної механіки швидкість обертання, а отже момент кількості руху, змінюються неперервно. У квантовій механіці проєкція моменту кількості руху на напрямок поля може набувати лише певних дискретних значень, які задаються певним квантовим числом, яке отримало назву магнітного квантового числа. Як наслідок, енергія атома чи молекули у стані з ненульовим орбітальним моментом розщеплюється на кілька дискретних рівнів. Про це розщеплення говорять як про зняття виродження.
Оскільки лінії оптичних спектрів пояснюються переходами між енергетичними рівнями, то розщеплення якогось із енергетичних рівнів призводить до відповідного розщеплення ліній оптичних спектрів. Якщо, наприклад, основний стан атома є невиродженим (s-станом), а переходи відбуваються в трикратно вироджений p-стан, то оптична лінія розщепиться на три близькі складові, які віддалятимуться при зростанні магнітного поля.
Математичне формулювання
Гамільтоніан квантовомеханічної системи з одним електроном у магнітному полі з магнітною індукцією записується у вигляді
- ,
де — частина гамільтоніану, яка не залежить від магнітного поля, — магнетон Бора, — оператор кутового моменту електрона, — оператор спіну електрона, — приведена стала Планка.
Загалом, оператор із врахуванням релятивістських ефектів залежить від спін-орбітальної взаємодії, але, щоб особливо не заплутатися розглядатимемо спочатку стани, в яких або спін або орбітальний момент дорівнює нулю.
- У випадку, коли спін системи дорівнює нулю, енергетичний рівень з орбітальним квантовим числом l та енергією розщепиться в магнітному полі на (2l+1) рівні:
- .
- У випадку, коли орбітальне квантове число дорівнює нулю, енергетичний рівень із спіном s та енергією розщепиться на (2s+1) рівні:
- ,
де — проєкція спіну на напрямок магнітного поля. У випадку електрона із спіном 1/2 рівнів буде 2.
У загальному випадку стану багатоелектронної задачі, із врахуванням спін-орбітальної взаємодії, і коли сумарний спін системи електронів не дорівнює нулю, ситуація складніша. Із міркувань симетрії за відсутності магнітного поля зберігається лише квадрат та одна із компонент повного моменту , причому всі енергетичні стани вироджені відносно магнітного квантового числа повного моменту . Прикладене магнітне поле знімає це виродження, проте величина розщеплення неодинакова для різних за природою енергетичних станів, а залежить від g-фактора Ланде цих станів. Деякі стани розщеплені навіть без прикладеного магнітного поля (це розщеплення називається мультиплетним або тонким розщепленням, наприклад, Електронні терми атомів)
Зееманівське розщеплення в оптичних спектрах
Лінії в оптичних спектрах відповідають переходам між енергетичними станами квантово-механічної системи. Розщеплення енергетичних рівнів у магнітному полі призводить до розщеплення оптичних ліній. Проте не всі переходи між енергетичними станами можливі. Деякі з них заборонені правилами відбору. Так, наприклад, магнітне квантове число не може змінитися при оптичному переході на 2, бо спін фотона всього лише одиниця, а при переході має виконуватися закон збереження моменту імпульсу. Як наслідок, в оптичних спектрах спостерігається менше ліній, ніж можна було б сподіватися. Крім того, зееманівське розщеплення в оптичному спектрі залежить від напрямку спостереження (відносно напрямку магнітного поля).
Нормальний ефект Зеемана
При спостереженні в перпендикулярному до поля напрямку оптична лінія розщеплюється на 3, відповідно до правила відбору
- .
Лінії при цьому поляризовані лінійно, крайні — перпендикулярно до магнітного поля, середня — паралельно до нього.
При спостереженні у напрямку магнітного поля середня лінія зникає, а дві крайні лінії поляризовані циркулярно: одна — за годинниковою стрілкою, інша — проти неї.
Така картина виникає в багатьох випадках і називається нормальним ефектом Зеемана.
Аномальний ефект Зеемана
У випадку, коли розщеплення електронних термів, між якими відбувається оптичний перехід, неоднакове за величиною, а залежить від множника Ланде, виникає аномальний ефект Зеемана, й число ліній в оптичному спектрі більше, ніж 3. На відміну від нормального ефекту Зеемана, аномальний ефект Зеемана неможливо пояснити за класичними уявленнями.
Сильні магнітні поля
Розщеплення ліній в оптичних спектрах пропорційне магнітному полю доти, доки лінії сусідніх атомних термів не починають перекриватися. У такому випадку складна картина аномального ефекту Зеемана поступово змінюється і в дуже сильних полях зводиться до трьох ліній, які відповідають нормальному ефекту Зеемана. Дане явище називається ефектом Пашена-Бака.
Застосування
Зееманівське розщеплення лежить в основі методів дослідження речовин, які використовуть магнітні резонанси: ЕПР, ЯМР, томографії тощо.
Див. також
Джерела
- Білий М. У., Охріменко Б. А. Атомна фізика. — К. : Знання, 2009. — 559 с.
- Глосарій термінів з хімії // Й.Опейда, О.Швайка. Ін-т фізико-органічної хімії та вуглехімії ім. Л. М. Литвиненка НАН України, Донецький національний університет — Донецьк: «Вебер», 2008. — 758 с. — ISBN 978-966-335-206-0
- Федорченко А. М. Квантова механіка, термодинаміка і статистична фізика // Теоретична фізика. — К. : Вища школа, 1993. — Т. 2. — 415 с.
- Юхновський І. Р. Основи квантової механіки. — К. : Либідь, 2002. — 392 с.
- Шпольский Э. В. Атомная физика (в 2-х томах). — М. : Наука, 1974. — 1024 с.