Ефект Штарка

Йоганнес Штарк відкрив явище розщеплення оптичних ліній в електричному полі в 1913 р., за що в 1919 р. отримав Нобелівську премію.

Зсуви Штарка першого та другого порядку у водні, магнітне квантове число: m = 1. Кожен n-рівень складається із n-1 вироджених підрівнів; наявність електричного поля знімає виродження.

Зміна енергії стаціонарних станів під впливом зовнішнього електричного поля залежить від того, чи в атому є дипольний електричний момент ${\displaystyle \mathbf {d} }$, чи ні. В першому випадку при включенні електричного поля з напруженістю ${\displaystyle \mathbf {E} }$ в наближенні, лінійному по полю, атом отримує додаткову енергію

${\displaystyle W=-(\mathbf {d} \cdot \mathbf {E} )}$

Тоді зміщення із розщепленням спектральних ліній буде також пропорційним першій степені напруженості ${\displaystyle \mathbf {E} }$. Таке розщеплення називають «лінійним ефектом Штарка».

Якщо атом не має власного електричного дипольного моменту, то в присутності електричного поля ${\displaystyle \mathbf {E} }$ він приймає середній електричний дипольний момент ${\displaystyle <\mathbf {d} >}$. Якщо зовнішнє поле є достатньо слабке, тобто воно значно менше електричного поля в атомах, яке створюють заряди ядра (не менше ${\displaystyle 10^{10}}$)В/м, то

${\displaystyle \left\langle \mathbf {d} \right\rangle =\alpha \mathbf {E} }$

де коефіцієнт пропорційності ${\displaystyle \alpha }$ називають поляризовністю атома. Для атомів із сферичною симетрією ${\displaystyle \alpha }$ — скаляр, а в загальному випадку він являє собою симетричний тензор. Поляризовність атому може бути обчислена методами квантової механіки. При збільшенні електричного поля від нуля до ${\displaystyle \mathbf {E} }$, дипольний момент атому також змінюється від нуля до ${\displaystyle \left\langle \mathbf {d} \right\rangle }$. При цьому над атомом здійснюється робота

${\displaystyle W={\frac {1}{2}}\left\langle \mathbf {d} \right\rangle \mathbf {E} ={\frac {1}{2}}\alpha \mathbf {E} ^{2}}$

котра йде на збільшення потенційної енергії атома в зовнішньому полі. Зміщення та розщеплення спектральних ліній в таких атомів пропорційне ${\displaystyle \mathbf {E} ^{2}}$. Таке розщеплення називають «квадратичним ефектом Штарка». Цей ефект менше лінійного. Атом, який має власний дипольний момент ${\displaystyle \mathbf {d} }$ в електричному полі, отримує і додатковий (індукований) дипольний момент, який в першому наближенні пропорційний ${\displaystyle \mathbf {E} }$. Відбувається накладка лінійного та квадратичного ефектів Штарка. Зміщення ліній виявляється несиметричним — вони зміщуються в червоний бік спектра, в область менших енергій. У воднеподібних атомів ефект Штарка лінійний. Це пояснюється тим, що в таких атомах електричне поле ядра, в якому рухаються електрони, є кулонівське, і його енергетичні рівні вироджені по ${\displaystyle l}$. Рівняння Шредінгера для воднеподібного атома в зовнішньому електричному полі ${\displaystyle E}$ має вигляд

${\displaystyle \left(-{\frac {h^{2}}{2\mu }}\Delta -{\frac {Ze^{2}}{r}}-ezE-W\right)\psi =0}$,

котрий відрізняється від стандартного наявністю члена ${\displaystyle -ezE}$, який обумовлений збуренням ${\displaystyle w_{0}}$ з боку поля. Тут враховано, що електричний момент атома з одним електроном ${\displaystyle \mathbf {d} =e\mathbf {r} }$, та вісь ${\displaystyle z}$ системи координат вибрана вздовж вектора напруженості електричного поля ${\displaystyle \mathbf {E} }$, тобто ${\displaystyle \mathbf {r} \mathbf {E} =zE}$. Величина ${\displaystyle \mu }$ — приведена маса електрона. Очевидно, що тут атом приймає аксіальну симетрію. Якщо величина поля мала, тобто коли зміна рівнів мала в порівнянні із відстанню між сусідніми рівнями без поля, то кількісна теорія ефекту Штарка може бути побудована на основі теорії збурень по збуренню ${\displaystyle w_{0}}$. В першому наближенні теорії збурень поправка ${\displaystyle \Delta W_{n}=W-W_{n}^{0}}$, де ${\displaystyle W}$ — енергія атома в полі, ${\displaystyle W_{n}^{0}}$ — енергія атома без поля, має вигляд:

${\displaystyle \Delta W_{n}=-e\mathbf {E} <r>_{n},<r>_{n}=\int _{}^{}\psi _{n}^{*}\mathbf {r} \psi _{n}\,d\mathbf {r} }$

де ${\displaystyle \psi _{n}}$ — власні функції, які відповідають власним значенням ${\displaystyle W_{n}^{0}}$ Хвильові функції ${\displaystyle \psi _{n}}$ будуються із врахуванням можливого виродження по ${\displaystyle l}$.

Основним станом атому водню є ${\displaystyle 1s-}$ (релятивістські ефекти не враховуються). Використавши явний вигляд хвильової функції для водню, можна показати, що ${\displaystyle <\mathbf {r} _{1}>=0}$, тобто в першому наближенні енергія основного стану в зовнішньому полі не змінюється. В першому збудженому стані ${\displaystyle n=2}$ необхідно врахувати виродження хвильової функції ${\displaystyle \psi _{2}}$ по ${\displaystyle l}$. Це можна зробити, записавши ${\displaystyle \psi _{2}}$ у вигляді лінійної комбінації функцій ${\displaystyle \psi _{nlm}}$ водню із квантовими числами ${\displaystyle n,l,m={2,0,0;2,1,0;2,1,1;2,1,-1}}$:

${\displaystyle \psi _{2}=\sum _{i=1}^{4}b_{i}\Phi _{i}}$

де позначено для простоти ${\displaystyle \Phi _{1}=\psi _{200},\Phi _{2}=\psi _{210},\Phi _{3}=\psi _{211},\Phi _{4}=\psi _{21-1}}$. Підставляючи останній вираз у рівняння Шредінгера для ${\displaystyle Z=1}$ та інтегруючи його із функціями ${\displaystyle \Phi _{i}^{*}}$, отримуємо систему рівнянь для коефіцієнтів ${\displaystyle b_{i}}$. Із умови розв'язності цієї системи знаходимо, що поправка до енергії ${\displaystyle \Delta W_{2}}$ може приймати три значення:

${\displaystyle \Delta W_{2}=3ea_{0}E,\Delta W_{2}=-3ea_{0}E,\Delta W_{2}=0}$

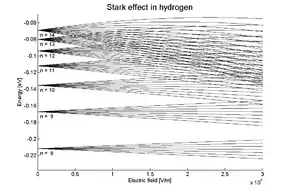
де ${\displaystyle a_{0}={\frac {h^{2}}{\mu e^{2}}}}$ — радіус Бора. Звідси випливає, що при включенні зовнішнього електричного поля чотирикратно вироджений рівень атома водню ${\displaystyle n=2}$ розщеплюється на три рівні. Стан із ${\displaystyle m=\pm \;1}$ є двократно виродженим. Величина розщеплення рівнів ${\displaystyle \Delta W_{n}}$ пропорційна напруженості електричного поля ${\displaystyle E}$. В загальному випадку рівень із головним квантовим числом ${\displaystyle n}$ в постійному електричному полі розщеплюється на ${\displaystyle n-2}$ підрівнів. У складніших атомах із одним валентним електроном поле, яке діє на зовнішній електрон, спотворене внутрішніми електронами і тому не є кулонівським. У такому полі виродження по ${\displaystyle l}$ немає. Можна показати, що в першому наближенні теорії збурень ${\displaystyle \Delta W_{n}=0}$ для кожного ${\displaystyle n}$ та ${\displaystyle l}$. В цьому випадку вплив електричного поля ${\displaystyle E}$ потрібно враховувати у другому порядку наближення теорії збурень, який приводить до величини розщеплення рівнів енергії атомів, квадратичної по полю ${\displaystyle E}$.

У випадку атома водню складовими, пропорційними ${\displaystyle E^{2}}$, можна знехтувати при ${\displaystyle E\leq \;10^{7}}$ В/м. При сильніших полях необхідно враховувати члени з ${\displaystyle E^{2}}$, а при ${\displaystyle E\sim \;4\cdot 10^{7}}$ — члени з ${\displaystyle E^{3}}$. Сьогодні ми маємо повну збіжність теорії з експериментом, до полів порядку ~${\displaystyle 10^{9}}$.

Спостерігається в напівпровідникових гетероструктурах, де матеріал з вузькою шириною зони знаходиться між двома матеріалами із широкими зонами. Як правило, драматично^{[що це?]} пов'язаний зі зв'язаними екситонами. Справа в тому, що електрони та дірки екситонів в електричному полі відштовхуються один від одного, проте все ж таки вони залишаються зв'язаними всередині області з вузькою зоною. Цей ефект широко використовується в напівпровідникових оптичних модуляторах, та в оптоволоконній оптиці.

• Ефект Зеемана
• Квантова точка
• Квантова дротина
• Квантова яма

• Білий М. У., Охріменко Б. А. Атомна фізика. — К. : Знання, 2009. — 559 с.
• Глосарій термінів з хімії // Й.Опейда, О.Швайка. Ін-т фізико-органічної хімії та вуглехімії ім. Л. М. Литвиненка НАН України, Донецький національний університет — Донецьк: «Вебер», 2008. — 758 с. — ISBN 978-966-335-206-0
• Вакарчук І. О. Квантова механіка. — 4-е видання, доповнене. — Л. : ЛНУ ім. Івана Франка, 2012. — 872 с.
• Юхновський І. Р. Основи квантової механіки. — К. : Либідь, 2002. — 392 с.
• Кузьмичёв В. Е. Законы и формулы физики. — К. : Наукова думка, 1989. — 864 с.

• Quantum Confined Stark Effect (QCSE) (англ.).