Зірчата область

Зірчата область, відносно фіксованої точки $x_{0}$ — область $D$ евклідового простору, $\mathbb {R} ^{n},$ така, що відрізок, що сполучає довільну точку області $D$ з точкою $x_{0}$ , цілком належить цій області.

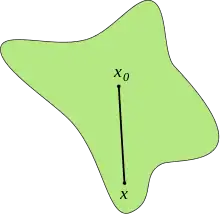
Зірчата область відносно точки

x_{0}

Кільце не є зірчатою областю

Формально, область $D\subseteq \mathbb {R} ^{n}$ називається зірчатою щодо точки $x_{0}\in D$ якщо для всіх точок $x\in D$ відрізок

[x_{0}\,x]=\left\{x_{0}+t(x-x_{0})\;\colon \;t\in [0,1]\right\}

повністю належить $D$ .

Приклади

Довільна лінія або площина в $\mathbb {R} ^{n}$ є зірчатою областю.
Довільна опукла область є зірчатою.
Область є опуклою тоді і тільки тоді, коли вона є зірчатою відносно кожної своєї точки.
Якщо A є множиною в $\mathbb {R} ^{n}$ , то множина $B=\{ta:a\in A,t\in [0,1]\}$ є зірчастою щодо початку координат.

Властивості

Зірчаста область є стягуваною множиною, зокрема вона є однозв'язною.
Непуста відкрита зірчата область $D\subseteq \mathbb {R} ^{n}$ є дифеоморфною $\mathbb {R} ^{n}.$
Непуста множина $D\subseteq \mathbb {R} ^{n}$ є зірчатою щодо точки $x_{0}$ тоді і тільки тоді коли її образ при перетворенні гомотетії з центром в точці $x_{0}$ і коефіцієнтом t є підмножиною $D$ для всіх $t\in \left[0,1\right]$ .
Підмножина $D$ дійсного векторного простору $E$ є зірчатою щодо точки $0$ тоді і тільки тоді коли існує функція $p:E\to \left[0,+\infty \right]$ для якої $\forall t\in \left[0,+\infty \right[\quad \forall x\in E\quad p(tx)=tp(x)$ , (приймається $0\times \infty =0$ ) і також $\{x\in E\mid p(x)<1\}\subset D\subset \{x\in E\mid p(x)\leqslant 1\}$ . Для відкритої множини $D=\{x\in E\mid p(x)<1\},$ для замкнутої $D=\{x\in E\mid p(x)\leqslant 1\},$ Ця функція є функціоналом Мінковського множини $D$ : $\forall x\in E\quad p(x)=\inf {\{\lambda >0\mid x\in \lambda D\}}$ . Зірчаста область щодо точки $0$ є обмеженою тоді і тільки тоді коли $p(x)>0,\quad x\in D,\;x\not =0.$ Вона є опуклою якщо $p(x+y)\leqslant p(x)+p(y).$

Див. також

Література

Касселс Дж., Введение в геометрию чисел, пер. с англ., М., 1965

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.