Стягуваний простір

Стягуваний простір — топологічний простір, гомотопно еквівалентний точці. Ця умова рівнозначна тому, що тотожне відображення на $X$ є гомотопним постійному.

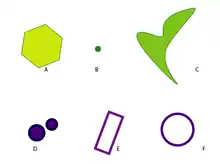
Простори A, B, і C є стягуваним; простори D, E, і F не є стягуваними.

Локально стягуваний простір — топологічний простір, кожна точка якого має базу з стягуваних околів. Еквівалентно якщо для кожної точки $x\in X$ і довільної відкритої підмножини $V\ni x$ простору $X$ , існує відкрита множина $U\ni x$ така що $U\subseteq V$ і $U$ є стягуваним простором у топології індукованій від $X$ .

Властивості

Простір $X$ є стягуваним тоді і тільки тоді, коли існує $x_{0}\in X$ таке, що $\{x_{0}\}$ — деформаційний ретракт простору $X$ .
Стягуваний простір завжди є однозв'язним; обернене твердження, в загальному випадку, не є правильним, стягуваність є сильнішим обмеженням, ніж однозв'язність.
Будь-яке неперервне відображення стягуваних просторів є гомотопною еквівалентністю. Два будь-яких неперервних відображень довільного простору в стягуваний простір є гомотопно еквівалентними; навпаки якщо два будь-які неперервні відображення в з деякого простору в $X$ є гомотопно еквівалентними, то $X$ — стягуваний простір.
Конус $\mathrm {C} X$ для даного простору $X$ — стягуваний простір, таким чином, будь-який простір $X$ може бути вкладеним в стягуваний простір і відповідно не кожен підпростір стягуваного простору є стягуваним. Крім того, $X$ є стягуваним тоді і тільки тоді, коли існує ретракція $\mathrm {C} X\to X$ .

Приклади і контрприклади

Прикладами стягуваних просторів є $n$ — вимірний дійсний простір $\mathbb {R} ^{n}$ , довільна опукла підмножина евклідового простору, зокрема - $n$ -вимірна куля.

Сфера в нескінченновимірному гільбертовому просторі є стягуваною, але при цьому $n$ -вимірні сфери не є стягуваними. Будь-яке неперервне відображення $n$ -вимірної сфери в стягуваний простір можна неперервно продовжити на $n+1$ -мірну куля.

Інші приклади стягуюваних просторів — многовид Ваайтхеда (тривимірний многовид, не гомеоморфний $\mathbb {R} ^{3}$ ), многовид Мазура (чотиривимірний гладкий многовид з краєм, що не є дифеоморфним чотиривимірній кулі).

Всі многовиди і CW-комплекси є локально стягуваними, але не є стягуваними в загальному випадку.
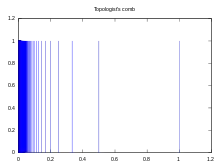
Локально стягувані простори не обов'язково є стягуваними. Прикладом є така підмножина $Y\subset \mathbb {R} ^{2}$ з індукованою топологією: $Y=\bigcup _{n\in \mathbb {N} }\{1/n\}\times [0,1]\bigcup \{0\}\times [0,1]\bigcup [0,1]\times \{0\}$ (див графік справа).

Література

О. Пришляк Топологія многовидів. — К., 2013. — 83 с.
Э. Спеньер. Алгебраическая топология. — М. : Мир, 1971. — С. 39-42.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.