Конциклічні точки
Конциклічні точки (або гомоциклічні точки) — точки, що лежать на одному колі. Три точки на площині, що не лежать на одній прямій, завжди лежать на одному колі, тому іноді термін «конциклічні» застосовують тільки до наборів з 4 або більше точок.[1]
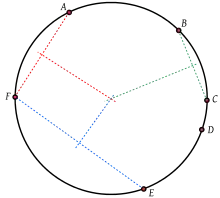

Серединні перпендикуляри
У загальному випадку центр O кола, на якому лежать точки P і Q, має бути таким, щоб відстані OP і OQ були рівними. Тому точка O має лежати на серединному перпендикулярі (або на медіатрисі) відрізка PQ.[2] Необхідною і достатньою умовою того, щоб n різних точок лежали на одному колі є те, що n(n − 1)/2 медіатрис відрізків, які з кінцями в будь-яких парах з n точок, всі одночасно перетиналися в одній точці, а саме: в центрі O.
Вписані многокутники
Трикутники
Вершини кожного трикутника лежать на колі[3]. Коло, що проходить через 3 вершини трикутника, називається описаним колом трикутника. Кілька інших наборів точок, які визначаються з трикутника, також лежать на одному колі, тобто є конциклічними точками; див. Коло дев'яти точок[4] і коло Лестер.[5]
Радіус кола, на якому міститься множина точок, за визначенням, є радіусом описаного кола будь-якого трикутника з вершинами в будь-яких трьох з цих точок. Якщо попарні відстані між будь-якими трьома з цих точок a, b і c, то радіус кола дорівнює
Рівняння описаного кола для трикутника, і вираз для радіуса і координат центру кола через декартові координати вершин наведено тут.
Чотирикутники
Чотирикутник ABCD з вершинами, що лежать на одному колі, називається вписаним; це буває тоді і тільки тоді, коли (за теоремою про кут, вписаний у коло), що виконується тоді і тільки тоді, коли протилежні кути чотирикутника доповнюють один одного до 180°.[6] Вписаний чотирикутник з послідовними сторонами a, b, c, d і півпериметром s = (a+b+c+d)/2 має радіус описаного кола, рівний[7][8]
Цей вираз отримав індійський математик Ватассері Парамешвара в XV столітті.
За теоремою Птолемея, чотирикутник, заданий попарними відстанями між його чотирма вершинами A, B, C і D відповідно, буде вписаним тоді і тільки тоді, коли добуток його діагоналей дорівнює сумі добутків протилежних сторін:
Якщо дві прямі, одна з яких містить відрізок AC, а інша містить відрізок BD, перетинаються в одній точці «Х», то ці чотири точки A, B, C, D є конциклічними точками тоді і тільки тоді, коли[9]
Точка перетину X може бути як всередині, так і поза описаним колом. Ця теорема відома як теорема про степінь точки.
n-кутники
У загальному випадку n-кутник, усі вершини якого лежать на одному колі, називається вписаним многокутником. Многокутник є вписаним многокутником, якщо і тільки якщо всі серединні перпендикуляри його сторін перетинаються в одній точці.[10]
Примітки
- Ефремов, 1902, с. 34.
- Libeskind, Shlomo (2008). Euclidean and Transformational Geometry: A Deductive Inquiry. Jones & Bartlett Learning. с. 21. ISBN 9780763743666./
- Elliott, John (1902). Elementary Geometry. Swan Sonnenschein & co. с. 126..
- Isaacs, I. Martin (2009). Geometry for College Students. Pure and Applied Undergraduate Texts 8. American Mathematical Society. с. 63. ISBN 9780821847947..
- Yiu, Paul (2010). The circles of Lester, Evans, Parry, and their generalizations. Forum Geometricorum 10: 175–209. MR 2868943..
- Pedoe, Dan (1997). Circles: A Mathematical View. MAA Spectrum (вид. 2nd). Cambridge University Press. с. xxii. ISBN 9780883855188..
- Alsina, Claudi; Nelsen, Roger B. (2007). On the diagonals of a cyclic quadrilateral (PDF). Forum Geometricorum 7: 147–9.
- Hoehn, Larry (March 2000). Circumradius of a cyclic quadrilateral. Mathematical Gazette 84 (499): 69–70. JSTOR 3621477.
- Bradley, Christopher J. (2007). The Algebra of Geometry: Cartesian, Areal and Projective Co-Ordinates. Highperception. с. 179. ISBN 1906338000. OCLC 213434422.
- Byer, Owen; Lazebnik, Felix; Smeltzer, Deirdre L. (2010). Methods for Euclidean Geometry. Mathematical Association of America. с. 77. ISBN 9780883857632..
Література
- Ефремов Дм. Новая геометрия треугольника. — Одесса, 1902.
