Крива Персея

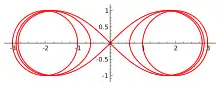
Крива́ Персе́я (спіричний перетин, спірична лінія, від дав.-гр. σπειρα — тор[1]) — лінія перетину поверхні тора площиною, паралельною до осі обертання тора; плоска алгебрична крива 4-го порядку[2]. Залежно від відстані січної площини до осі тора, криві можуть мати форми «опуклих» та «увігнутих» овалів, «вісімок» та двох окремих овалів[3].

Криві Персея як переріз тора площиною

Три кривих Персея:
${\displaystyle a=1,b=2,c=0}$
${\displaystyle a=1,b=2,c=0{,}8}$
${\displaystyle a=1,b=2,c=1}$

Вперше цей підклас торичних перерізів вивчався давньогрецьким геометром Персеєм близько 150 року до н. е., через приблизно 200 років після перших досліджень конічних перетинів Менехмом[4]. Повторно описані у XVII столітті[3] лемніската Бута («опуклий овал») і овал Кассіні («вісімка») — є частковими випадками кривої Персея.

Рівняння кривої у декартовій системі координат[5]:

${\displaystyle (x^{2}+y^{2})^{2}=ax^{2}+by^{2}+c}$.

Інша форма рівняння у декартових координатах:

${\displaystyle (r^{2}-a^{2}+c^{2}+x^{2}+y^{2})^{2}=4r^{2}(x^{2}+c^{2})}$,

тут ${\displaystyle a}$ — радіус кола, обертанням якого уздовж кола з радіусом ${\displaystyle r}$ утворений тор. При ${\displaystyle c=0}$ крива складається з двох кіл радіуса ${\displaystyle a}$ з центрами ${\displaystyle (\pm r,0)}$; при ${\displaystyle c=r+a}$ крива вироджується у точку — початок координат, якщо ж ${\displaystyle c>r+a}$ — то крива складається з порожньої множини точок[4].

Також можна визначити криву Персея як біциркулярну криву[6], симетричну відносно осей ${\displaystyle x}$ і ${\displaystyle y}$.

Рівняння у полярних координатах:

${\displaystyle (r^{2}-a^{2}+b^{2}+c^{2})^{2}=4b^{2}(r^{2}\cos ^{2}\theta +c^{2})}$,

або

${\displaystyle r^{4}=dr^{2}\cos ^{2}\theta +er^{2}\sin ^{2}\theta +f}$.