Лемніската

Назва «лемніската» походить від дав.-гр. λημνίσκος — стрічка, пов'язка. В Стародавній Греції «лемніскатою» називали бантик, за допомогою якого прикріплювали вінок до голови переможця спортивних ігор.

• Лемніскатою з одним фокусом (${\displaystyle n=1}$) є коло радіусу ${\displaystyle r}$, а з двома фокусами — овал Кассіні.
• Окремим випадком овалу Кассіні є лемніската Бернуллі, названа на честь швейцарського математика Якоба Бернуллі, який поклав початок вивченню лемніскат.

• Рівняння лемніскати на комплексній площині має вигляд

${\displaystyle \left|(z-z_{1})(z-z_{2})\ldots (z-z_{n})\right|=r^{n},\;z=x+iy,\;r>0.}$

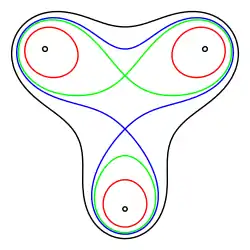
Довільну криву можна наблизити послідовністю лемніската. Зокрема, беручи різну кількість фокусів, розташовуючи їх по-різному і призначаючи ту чи іншу величину для добутку відстаней, можна отримувати лемніскати найхимерніших обрисів, наприклад, обриси людської голови або птиці.

Лемніска́та Берну́ллі — крива, добуток відстаней кожної з точок якої до двох фокусів дорівнює квадрату половини відстані між фокусами. Ця лінія за формою нагадує вісімку. Автор цієї кривої, швейцарський математик Якоб Бернуллі, дав їй поетичну назву «лемніската». В античному Римі так називали бантик, за допомогою якого прикріплювали вінок до голови переможця у спортивних іграх.

Рівняння лемніскати Бернуллі

Рівняння лемніскати Бернуллі в прямокутних координатах:

${\displaystyle (x^{2}+y^{2})^{2}-2a^{2}(x^{2}-y^{2})=0,}$

Рівняння в полярних координатах:

${\displaystyle \rho ^{2}=2a^{2}\cos(2\phi ).}$

• Лемніската Бута
• Лемніската Бернуллі
• Овал Кассіні
• Плоска крива
• Алгебрична крива
• Дивний атрактор Лоренца
• Точка зчленування (топологія)
• Поліноміальна лемніската
• Стала Гауса

• Математическая энциклопедия (в 5 томах). — М. : "Советская Энциклопедия". — Т. 3 (Коо-Од). — С. 234.
• Маркушевич А. И. Замечательные кривые. — Гостехиздат, 1952. — 32 с. — (Популярные лекции по математике, выпуск 4). Архівовано вересень 14, 2008 на сайті Wayback Machine.

• Савелов А. А. Плоские кривые / Под. ред. А. П. Нордена. — М. : ФИЗМАТГИЗ, 1960. — С. 155-162.(рос.)