Лемніската Бернуллі
Лемніската Бернуллі — геометричне місце точок, добуток відстаней від яких до двох заданих точок (фокусів) незмінна і дорівнює квадрату половини відстані між фокусами.

Назва походить з античного Риму, де «лемніскатою» називали бантик, з допомогою якого прикріпляли вінок до голови переможця на спортивних іграх. Цю лемніскату називають в честь швейцарського математика Якоба Бернуллі, який поклав початок її вивченню.
Рівняння
Розглянемо простий випадок: якщо відстань між фокусами , розташовані вони на осі , і початок координат ділить відрізок між ними навпіл, то наступні рівняння задають лемніскату:
Фокуси лемнискати — і . Візьмемо довільну точку . Добуток відстаней від фокусів до точки є
- ,
і за означенням вона дорівнює :
Піднесемо в квадрат дві частини рівності:
Розкриємо дужки в лівій частині:
Розкриємо дужки і згорнемо новий квадрат суми
Винесемо спільний множник і перенесемо:
Далі можна зробити заміну :
В даному випадку — радіус поверхні, що описує лемніскату.
- Зробивши нескладні перетворення, можна отримати рівняння у явному вигляді:
Піднесемо в квадрат і розкриємо дужки:
Приведемо до вигляду
Це квадратне рівняння відносно . Розв'язавши його, отримаємо
Взявши корінь і відкинувши варіант з від'ємною другою змінною, отримаємо:
де додатній варіант визначає верхню половину лемніскати, від'ємний — нижню.
Використовуючи формули переходу до полярної системи координат отримаємо:
Винесемо спільні множники і використаємо тригонометричну тотожність :
Використаємо ще одну тотожність: :
Поділимо на , вважаючи, що :
Як і в випадку прямокутної системи можна замінити :
- Параметричне рівняння в прямокутній системі:
- , де
Щоб задати лемніскату по двох довільних точках, можна не виводити рівняння заново, а визначити перетворення координат, при якому старий (даний) фокусний відрізок переходить в новий, і подіяти на представлені рівняння цим перетворенням.
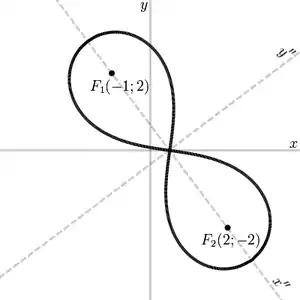
Нехай, наприклад, — фокуси.
Існує прямокутна система координат (на малюнку — ), в якій рівняння лемніскати має вигляд
Необхідно визначити перетворення системи координат, що переводить в . Це перетворення здійснюється в два етапи: паралельне перенесення і поворот.
Середина відрізка — , значить перенос тільки на по осі :
Після переносу системи координат її потрібно повернути на деякий кут. Для визначення кута спочатку знайдемо відстань між фокусами:
значить .
Тепер із геометричних міркувань знайдемо синус і косинус кута нахилу к :
Формули перетворення:
Поєднавши обидва перетворення, отримаємо скінченні формули переходу:
Для того, щоб отримати рівняння в стандартній системі координат, підставимо ці співвідношення в вихідне рівняння кривої:
Після перетворень:
Це рівняння задає лемніскату з фокусами в стандартній прямокутній системі координат.
Властивості
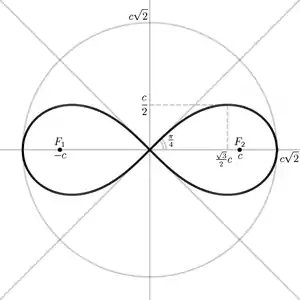
- Лемніската — крива четвертого порядку.
- Вона має дві осі симетрії: пряма, на якій лежить , і серединний перпендикуляр цього відрізка, в простішому (даному) випадку — вісь .
- Точка, де лемниската перетинає саму себе, називається вузловою чи подвійною точкою.
- Крива має 2 максимуми і 2 мінімуми. Їх координати:
- Відстань від максимуму до мінімуму, що знаходяться по одну сторону від серединного перпендикуляра (осі в даному випадку) дорівнює відстані від максимуму (чи від мінімуму) до подвійної точки.
- Дотичні в подвійній точці складають з відрізком кути .
- Лемніскату описує поверхня радіуса , тому деколи в рівняннях проводять цю заміну.
- Інверсія відносно поверхні з центром в подвійній точці, переводить леминіскату Бернуллі в рівнобічну гіперболу.
- В полярних координатах , вірне наступне
- Площа полярного сектора , при :
- Площа кожної петлі .
- Радіус кривини лемніскати є
- Площа полярного сектора , при :
Рівняння лемніскати в полярній системі:
Формули переходу до полярної системи координат:
Виразимо :
Підставимо в рівняння лемнискати і виразимо і :
—- це параметричне рівняння відносно . Проводячи деякі тригонометричні перетворення, можна отримати рівняння відносно Формула радіуса кривизни кривої, заданої параметрично:
Знайдемо похідні по :
Підставимо в формулу радіуса:
Повернемося до рівняння лемніскати:
Підставимо цей вираз в отриману формулу радіуса і отримаємо:
Побудова
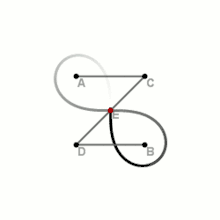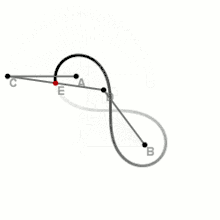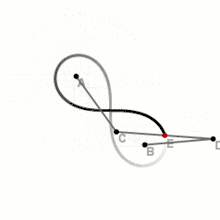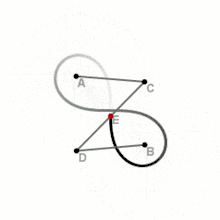
З допомогою трьох відрізків
Це один із найбільш простих і швидких способів, однак потребує наявності додаткових пристосувань.
На площині вибираються дві точки — і — наступні фокуси лемніскати. Складається спеціальна конструкція із трьох скріплених в ряд на шарнірах відрізках, щоб отримана лінія могла вільно вигинатися в двох містах (точки вигину — и ). При цьому необхідно зберігати пропорції відрізків: . Краї лінії закріплюються до фокусів. При непараллельному повертанні відрізків навколо фокусів середина центрального відрізка описує лемніскату Бернуллі.
