Моделювання твердих тіл
Моделюва́ння тверди́х тіл являє собою послідовний набір принципів математичного та комп'ютерного моделювання тривимірних твердих тіл. Твердотільне моделювання відрізняється від суміжних областей геометричного моделювання та комп'ютерної графіки наголосом на фізичних властивостях.[1] Разом, принципи геометричного і твердотільного моделювання є основою автоматизованого проектування і загальної підтримки створення, обміну, візуалізації, анімації, опису і анотування цифрових моделей фізичних об'єктів.

Огляд
Застосування твердих методів моделювання дозволяє автоматизувати кілька складних інженерних розрахунків, які проводяться як частина процесу проектування. Моделювання, планування і перевірка процесів, таких як обробка було одним з основних каталізаторів для розвитку твердотільного моделювання. Зовсім недавно, діапазон програм, які підтримуються на виробництвах було значно розширено, щоб забезпечити виготовлення листового металу, лиття під тиском, зварювання, будування труб. Крім традиційного виробництва, тверді методи моделювання є основою для швидкого прототипування, цифрових архівних даних і зворотного проектування за допомогою відновлення твердих частинок з вибіркових точок на фізичних об'єктах, з використанням механічного аналізу кінцевих елементів, кінематичний і динамічний аналіз механізмів, і так далі. Головною проблемою у всіх цих додатків є здатність ефективно представляти та маніпулювати тривимірну геометрію таким чином, що узгоджується з фізичною поведінкою реальних артефактів. Дослідження і розробка моделювання твердих тіл ефективно вирішило багато з цих питань, і продовжує залишатися в центрі уваги комп'ютерного проектування.
Математичні основи
Поняття твердотільного моделювання, як це практикується сьогодні, залежить від конкретної необхідності інформаційної повноти в механічних системах геометричного моделювання, в тому сенсі, що будь-яка комп'ютерна модель повинна підтримувати всі геометричні запити, які можуть бути задані його відповідним фізичним об'єктом. Вимога побічно визнає можливість кількох комп'ютерних уявлень одного і того ж фізичного об'єкта до тих пір, як будь-які два таких уявлення узгоджуються. Неможливо підрахунками перевірити інформаційну повноту уявлення, якщо поняття фізичного об'єкта не визначене в термінах обчислюваних математичних властивостей і не залежить від будь-якого конкретного уявлення. Такі міркування привели до розробки парадигми моделювання, що сформувало поле твердотільного моделювання, як ми його знаємо сьогодні.
Всі виготовлені компоненти мають скінченні розміри і добре виражені межі, тому спочатку акцент був зроблений на математичному моделюванні жорстких деталей з однорідного ізотропного матеріалу, який може бути доданий або видалений. Ці властивості можуть бути переведені на властивості підмножин тривимірного евклідового простору. Два загальних підходи до визначення міцності покладаються на теоретико-множинну топологію і алгебраїчну топологію відповідно. Обидві моделі визначають, як тверді частини можуть бути побудовані з простих частин або елементів.
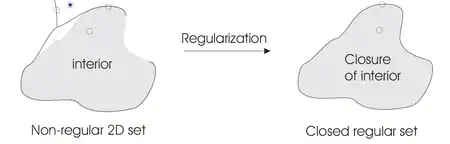
Всі точки будь-якого X ⊂ ℝ3 можуть бути класифіковані відповідно до їх околу по відношенню до X, як внутрішні, зовнішні або граничні точки. Припускаючи, що ℝ3 наділена типовою евклідовою метрикою, окіл точки p ∈X приймає форму відкритої кулі. Для X, щоб вважати твердим, кожна околиця будь-якого p ∈X повинна бути послідовно тривимірною; точки з більш низькими мірними околицями вказують на відсутність монолітності. Розмірна однорідність околиць гарантуються для класу замкнутих регулярних множин, визначається як множину рівних із замиканням їх інтер'єру. Будь-який X ⊂ ℝ3 може бути перетворений в закриту регулярну множину або регуляризується замикання свого інтер'єру, і, таким чином, моделювання простору твердих речовин математично визначається як простір замкнутих регулярних підмножин ℝ3 (по теоремі Гейне-Бореля). Крім того, тверді речовини, повинні бути закриті під булевими операціями множин об'єднання, перетину і різниці (щоб гарантувати міцність після додавання матеріалів і видалення). Застосовуючи стандартні логічні операції для замкнутих регулярних множин можуть не утворити замкнуту регулярну множину, але ця проблема може бути вирішена шляхом регуляризації результатів застосування стандартних логічних операцій. Врегульований набір операцій позначаються ∪∗, ∩∗, і −∗.
Комбінаторна характеристика множини X ⊂ ℝ3 як твердого тіла включає в себе X, що представляється як клітинний комплекс орієнтований таким чином, що клітини забезпечують скінченні просторові адреси для точок в іншому незліченному континууму. Клас напіваналітичного обмежених підмножин евклідового простору замкнуто щодо булевих операцій і володіє додатковою властивістю, що кожна напіваналітична множина може бути розділена на сукупність непересічних клітин розмірів 0,1,2,3. Триангуляція (топологія) напіваналітичної множини в сукупність точок, відрізків, трикутних граней і тетраедричних елементів є прикладом стратифікації, яка зазвичай використовується. Комбінаторна модель монолітності також підсумована тим, що в доповненні до напіваналітичної обмеженої підмножини, тверді частинки є тривимірними топологічними багатогранниками, зокрема тривимірних. Модель комбінаторного різноманіття монолітності також гарантує кордон простору твердих розділених на дві компоненти рівно як наслідок теореми Жордана-Брауера, таким чином, усуваються множини з не різноманітними районами, які неможливо виготовити.
Множина точок і комбінаторні моделювання твердих тіл повністю узгоджуються один з одним, вони можуть бути використані як взаємозамінні, спираючись на континуумі або комбінаторних властивостей за потребою, і може бути розширений до n вимірювань. Ключова властивість, що полегшує цю послідовність в тому, що клас замкнутих регулярних підмножин ℝn точно збігаються з однорідно n-вимірними топологічними багатогранниками. Таким чином, кожне n-вимірне тверде тіло може бути однозначно представлене його межею, а межа має комбінаторну структуру n−1-мірного многогранника, що має однорідну n−1-мірні межу.
Схеми представлення твердих тіл
На підставі прийнятих математичних властивостей, будь-яка схема, яка представляє тверді тіла являє собою спосіб для збору інформації про клас напіваналітичної підмножини евклідового простору. Це означає, що всі представлення є різними способами організації тих же геометричних і топологічних даних у вигляді структури даних. Всі представлення організовані в термінах скінченного числа операцій на безлічі примітивів. Таким чином, моделювання простору будь-якого конкретного представлення скінченна, і будь-якого одного представлення схеми може бути не повністю достатньо, щоб представляти всі типи твердих тіл. Наприклад, тверді речовини, визначені за допомогою комбінацій булевих операцій, вони можуть не обов'язково бути представлені в розгорнутому вигляді примітивного переміщення відповідно до просторової траєкторії, за винятком дуже простих випадків. Це змушує сучасні системи геометричного моделювання до підтримки кількох схем представлення твердих тіл, а також до полегшення ефективного перетворення між схемами уявлення.
Нижче наведено список найбільш поширених методів, використовуваних для створення або являють собою твердотільні моделі. Сучасне програмне забезпечення для моделювання може використовувати комбінацію цих схем для подання твердого тіла.
Параметризовані примітивні інстанси
Ця схема заснована на русі сімейств об'єктів, кожен член сім'ї відрізняється від іншого за кількома параметрами. Кожна сім'я об'єктів називається загально примітивною, і окремі об'єкти всередині сімейства називаються примітивними екземплярами. Наприклад, сімейство болтів є загально примітивним, і один болт, що задається певним набором параметрів є примітивним екземпляром. Відмітна риса чистих параметризованих схем інстансу є відсутність коштів для об'єднання примірників, щоб створити нові структури, які являють собою нові більш складні об'єкти. Іншим основним недоліком цієї схеми є труднощі написання алгоритмів для обчислення властивостей, представлених твердих тіл. Значна кількість інформації про конкретну сім'ю повинно бути вбудовано в алгоритми і тому кожен загальний примітив має розглядатися як окремий випадок, не дозволяючи рівномірне загальне обчислення.
Просторове розміщення перерахування
Ця схема являє собою список з просторових осередків, зайнятих твердим тілом. Клітини є кубом фіксованого розміру і розташовані в фіксованій просторовій сітці (інші багатогранні механізми також можливі, але кубики є самим простими). Кожна клітинка може бути представлена координатами однієї точки, наприклад, центроїда клітини. Як правило, конкретний порядок сканування накладається і відповідний упорядкований набір координат називається просторовим масивом. Просторові масиви є однозначними і унікальними представленнями твердих тіл, але занадто багатослівні для використання в ролі «майстрів». Однак, вони можуть бути використані для підвищення продуктивності геометричних алгоритмів, особливо при використанні в поєднанні з іншими представленнями, такими як конструктивна блокова геометрія.
Розбиття клітин
Ця схема випливає з описів комбінаторних властивостей твердих тіл, описаних вище. Тверде тіло може бути представлене його розбиттям на декілька клітин. Просторові схеми розміщення перерахувань є окремим випадком клітинного розбиття, де всі клітини є кубічними і лежать в регулярній сітці. Клітинне розбиття забезпечує зручні способи для обчислення певних топологічних властивостей твердих речовин, такі, як його зв'язаність і рід. Інші розкладання клітин можуть бути використані для застосування в плануванні рухів робота.
Граничне представлення
Часто позначається як B-rep або BREP, — спосіб представлення фігур за допомогою їхніх границь. Тверде тіло являє собою сукупність взаємопов'язаних елементів поверхні — границь між тілом і навколишнім простором.
Моделювання поверхонь сітки
Аналогічно до граничного представлення, використовується проста поверхня з вершинами і ребрами. Поверхня сітки може бути структурована або неструктурована трикутниками або полігонами вищого рівня.
Конструктивна блокова геометрія
Конструктивна блокова геометрія часто, але не завжди, є способом моделювання в тривимірній графіці та САПР. Вона дозволяє створити складну сцену або більш складний об'єкт, як комбінацію інших об'єктів за допомогою бітових операцій. Це дозволяє спростити математичний опис складних об'єктів, хоча для цього не завжди використовуються лише прості тіла. Так, часто за допомогою конструктивної блокової геометрії представляють моделі або поверхні, які лише виглядають складними, а насправді, вони являють собою більш хитро скомбіновані або де комбіновані прості об'єкти. В деяких випадках конструктивна блокова геометрія використовує полігональні сітки (англ. polygonal mesh), і може бути процедурною та/або параметричною.
Підмітання
Основна ідея втілюється в широких схемах просто. Множина рухається через простір «замітає» обсяг (тверде тіло), який може бути представлений в русі і встановити його траєкторію. Таке уявлення має важливе значення в контексті додатків, такі як виявлення матеріалу видаленого з різального пристрою, як він рухається уздовж заданої траєкторії, обчислення динамічної інтерференції двох твердих тіл, зазначених відносним рухом, планування руху, і навіть в комп'ютерних графічних додатках, такі як відстеження руху пензля, що рухається на полотні. Сучасні дослідження показали кілька наближень тривимірних фігур, що рухаються по одному параметру, і навіть рухів декількох параметрів.
Неявне представлення
Вельми загальний метод визначення множини точок X, для вказання предикату, який може бути оцінений в будь-якій точці простору. Іншими словами, X визначається неявно і складається з усіх точок, що задовольняють умові, заданого предиката. Найпростіша форма предиката є умова про ознаку речової функції, що призводить до знайомого уявлення про множини рівностей і нерівностей.
Параметричні функції на основі моделювання
Особливості визначаються як параметричні форми, пов'язані з атрибутами, такими як власні геометричні параметри (довжина, ширина, глибина тощо), положення і орієнтація, геометричні допуски, властивості матеріалів, а також посилання на інші функції. Можливості програми також забезпечують доступ до супутніх виробничих процесів і моделям ресурсів. Таким чином, особливості мають семантичний вищий рівень, ніж примітивні замкнуті регулярні множини. Характеристики, як правило, передбачаються сформувати для організації баз даних для повторного використання проектних даних. Параметричне моделювання на основі функції часто поєднується з конструктивною бінарною твердою геометрією (CSG) для повного опису систем складних об'єктів в машинобудуванні.
Історія моделювання твердих тіл
Історичний розвиток моделювання твердих тіл слід розглядати в контексті всієї історії САПР, основні віхи є розвитком дослідницької системи BUILD з подальшою її комерційним виділенням Romulus, який продовжував впливати на розвиток Parasolid, ACIS і об'ємне моделювання рішень. Один з перших розробників САПР в Співдружності Незалежних Держав (СНД), АСКОН почав внутрішній розвиток свого власного моделювання твердих тіл в 1990 році. У листопаді 2012 року, математичний розподіл АСКОН став окремою компанією, і був названий c3d Labs. Їй була поставлена задача розробки C3D геометричного моделювання ядра як окремого продукту. Інші внески прийшли з Туукка Мянтюля, з його GWB і від проекту GPM що сприяло, зокрема, розвитку гібридних методів моделювання на початку 1980-х років.
Двовимірне параметричне креслення і моделювання
Параметризація двовимірних креслень зазвичай доступна в CAD-системах середнього і тяжкого класів. Хоча наголос в цих системах зроблений на тривимірну технологію проектування, і можливості параметризації двовимірних креслень практично не використовується. Параметричні CAD-системи, орієнтовані на двовимірне креслення (легкий клас), частіше за все є «урізаними» версіями сучасніших САПР.
Тривимірне твердотільне параметричне моделювання
Тривимірне параметричне моделювання являє собою набагато більш ефективний (але і більш складний) інструмент, ніж двовимірне параметричне моделювання. В сучасних САПР середнього і тяжкого класів наявність параметричної моделі закладено в ідеологію самих САПР. Існування параметричного опису об'єкту являє собою базу для всього процесу проектування.
Див. також
Примітки
- Shapiro, Vadim (2001). Solid Modeling. Elsevier. Процитовано 20 квітня 2010.