Міра Жордана

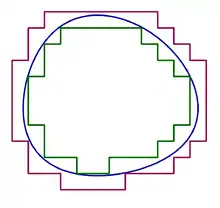
Множина вимірна за Жорданом, якщо внутрішня міра Жордана дорівнює зовнішній мірі Жордана.

Міра Жордана ${\displaystyle ~m(\Delta )}$, добутку напівінтервалів ${\displaystyle \Delta =\prod _{i=1}^{n}[a_{i},\;b_{i})}$ в ${\displaystyle \mathbb {R} ^{n}}$ визначається як добуток

${\displaystyle m(\Delta )=\prod _{i=1}^{n}(b_{i}-a_{i}).}$

Для обмеженої множини ${\displaystyle E\subset \mathbb {R} ^{n}}$ визначаються:

• зовнішня міра Жордана

  ${\displaystyle m_{e}(E)=\inf \sum _{k=1}^{N}m(\Delta _{k}),\quad \bigcup _{k}\Delta _{k}\supset E}$

• внутрішня міра Жордана

  ${\displaystyle m_{i}(E)=\sup \sum _{k=1}^{N}m(\Delta _{k}),\quad \bigcup _{k}\Delta _{k}\subset E,\quad \Delta _{k}\cap \Delta _{m}=\varnothing }$, якщо ${\displaystyle \ k\neq m,}$

де ${\displaystyle \Delta _{1},\;\Delta _{2},\;\ldots ,\;\Delta _{N}}$ — паралелепіпеди описаного вище виду.

Множина ${\displaystyle ~E}$ називається вимірною за Жорданом, якщо ${\displaystyle ~m_{e}(E)=m_{i}(E)}$. В цьому випадку міра Жордана дорівнює ${\displaystyle ~m(E)=m_{e}(E)=m_{i}(E)}$.

• Міра Жордана інваріантна щодо рухів евклідового простору.
• Обмежена множина ${\displaystyle E\subset \mathbb {R} ^{n}}$ вимірна за Жорданом тоді і тільки тоді, коли її границя має міру Жордана рівну нулю.
• Зовнішня міра Жордана для ${\displaystyle ~E}$ рівна зовнішній мірі Жордана для ${\displaystyle {\bar {E}}}$ (замикання множини ${\displaystyle ~E}$) і рівна мірі Бореля ${\displaystyle {\bar {E}}}$.
• Вимірні за Жорданом множини утворюють кільце множин, на якому міра Жордана є скінченно-адитивною функцією.

Усі прямокутники, кулі, симплекси є вимірними за Жорданом. Простим прикладом не вимірної за Жорданом множини є множина раціональних чисел. Зовнішня міра Жордана цієї множини дорівнює 1, а внутрішня дорівнює нулю.

• Peano, G. Applicazioni geometriche del calcolo infinitesimale. — Torino, 1887;
• Jordan, C. Journal de Mathématiques Pures et Appliquées. — 1892. — t. 8. — p. 69—99;

• Міра Лебега
• Міра множини
• Міра Хаусдорфа
• Міра Бореля