Нульовий морфізм

Нехай C — категорія, і f : X → Y — морфізм в C. F називається постійним морфізмом, якщо для будь-якого об'єкта W в C і будь-яких g, h : W → X, fg = fh. Відповідно, f називається копостійним морфізмом, якщо для будь-якого об'єкта Z і будь-яких g, h ∈ Mor_C(Y, Z), gf = hf.

Нульовий морфізм — морфізм, що є одночасно постійним і копостійним.

Категорія з нульовими морфізмами — категорія, в якій для будь-яких двох об'єктів A і B зафіксований морфізм 0_AB : A → B, такий що для будь-яких об'єктів X, Y, Z в C і будь-яких морфізмів f : Y → Z, g : X → Y діаграма нижче є комутативною:

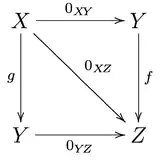
Тоді морфізм 0_XY обов'язково є нульовими. Якщо C — категорія з нульовими морфізмами, то 0_XY визначені однозначно.

• У категорії груп (або модулів) нульовий морфізм — це гомоморфізм f : G → H, що відображає всі елементи G в нейтральний елемент H. Нульовим об'єктом в категорії груп є тривіальна група 1 = {1}. Кожен нульовий морфізм розкладається через 1, тобто f : G → 1 → H.

• Більш загально, нехай C — категорія з нульовим об'єктом 0. Тоді для будь-яких двох об'єктів X і Y існує єдина послідовність морфізмів

0_XY : X → 0 → Y

сім'я таких морфізмів задає на C структуру категорії з нульовими морфізмами.

• Якщо C — передадитивна категорія, то кожна множина морфізмів Mor ( X, Y) є абелевою групою і має нульовий елемент. Ці нульові елементи утворюють сім'ю нульових морфізмів, і C є категорією з нульовими морфізмами.

• Категорія множин не має нульового об'єкта, але має початковий об'єкт, порожня множина ∅. Єдиними копостійними функціями у Set є функції виду ∅ → X.

• Pareigis, Bodo (1970). Categories and functors. Pure and applied mathematics 39. Academic Press. ISBN 978-0-12-545150-5.
• Herrlich, Horst; Strecker, George E. (1973). Category Theory. Allen and Bacon, Inc. Boston.