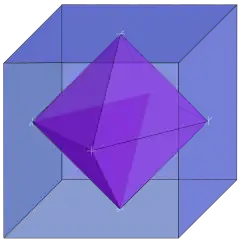
Багатогранник Ганнера

Багатогранники Ганнера — клас опуклих багатогранників, які можна отримати рекурсивно з відрізка за допомогою двох операцій: взяття прямого добутку і перехід до двоїстого багатогранника.

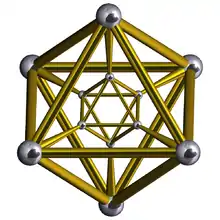
Куб і двоїстий йому октаедр — два тривимірних багатогранники Ганнера.
Чотиривимірна восьмигранна призма — перший приклад неправильного багатогранника Ганнера.

Названі на честь Олофа Ганнера, який розглянув їх 1956 року.[1]

Побудова

Багатогранники Ганнера утворюють мінімальний клас багатогранників, що задовольняє таким умовам:[2]

  • Відрізок прямої є одновимірним багатогранником Ганнера.
  • Прямий добуток двох багатогранників Ганнера є багатогранником Ганнера. (Його розмірність дорівнює сумі розмірностей двох початкових багатогранників.)
  • Багатогранник, двоїстий до багатогранника Ганнера є багатогранником Ганнера. (Цей багатогранник має ту ж розмірність, що й початковий.)

Зауваження
  • Замість операції переходу до двоїстого багатогранника можна брати опуклу оболонку об'єднання багатогранників, що містяться в перпендикулярних підпросторах.[3][4]

Приклади
  • Квадрат — це багатогранник Ганнера як прямий добуток двох відрізків.
  • Куб — це багатогранник Ганнера як прямий добуток трьох відрізків.
  • Октаедр — також багатогранник Ганнера як багатогранник, двоїстий до куба.

В розмірності три будь-який багатогранник Ганнера комбінаторно еквівалентний одному з цих двох видів багатогранників.[5] У вищих вимірах аналоги куба і октаедра, гіперкуби і гіпероктаедри, також є багатогранниками Ганнера. Однак є й інші приклади. Зокрема восьмигранна призма — чотиривимірна призма, в основі якої октаедр. Вона є багатогранником Ганнера, як добуток октаедра на відрізок.

Властивості
  • Багатогранники Ганнера центрально-симетричні.
  • Будь-який багатогранник Ганнера комбінаторно еквівалентний багатограннику з координатами будь-якої вершини, що набувають значень 0, 1 або −1.[6]
  • Загальне число граней -вимірного багатогранника Ганнера дорівнює .
  • Протилежні грані багатогранника Ганнера не перетинаються, і разом містять усі вершини багатогранника.
    • Зокрема, опукла оболонка двох таких граней є весь багатогранник.[6][7]
      • Як наслідок, усі грані багатогранника Ганнера мають однакове число вершин.
        • Однак грані можуть не бути ізоморфними одна одній. Наприклад, у восьмигранній 4-призмі дві грані є октаедрами, а решта вісім граней — трикутними призмами.
    • Двоїста властивість полягає в тому, що протилежні вершини суміжні з усіма гранями багатогранника.
  • Об'єм Малера, тобто добуток об'ємів самого багатогранника і його двоїстого, для багатогранника Ганнера той самий, що у й куба.
    • Гіпотеза Малера полягає в тому, що серед центрально-симетричних опуклих тіл цей об'єм досягає мінімуму на багатогранниках Ганнера.[8]
  • Число комбінаторних типів багатогранників Ганнера розмірності d таке саме, як число послідовно-паралельних графів з d ребрами.[4] Для d = 1, 2, 3, …, це послідовність A058387 з Онлайн енциклопедії послідовностей цілих чисел, OEIS.
    1, 1, 2, 4, 8, 18, 40, 94, 224, 548, …

Примітки
  1. Hanner, Olof (1956). Intersections of translates of convex bodies. Mathematica Scandinavica 4: 65–87. MR 0082696..
  2. Freij, Ragnar (2012). Topics in algorithmic, enumerative and geometric combinatorics. Ph.D. thesis. Department of Mathematical Sciences, Chalmers Institute of Technology..
  3. Kalai, Gil (1989). The number of faces of centrally-symmetric polytopes. Graphs and Combinatorics 5 (1): 389–391. MR 1554357. doi:10.1007/BF01788696..
  4. Sanyal, Raman; Werner, Axel; Ziegler, Günter M. (2009). On Kalai's conjectures concerning centrally symmetric polytopes. Discrete & Computational Geometry 41 (2): 183–198. MR 2471868. doi:10.1007/s00454-008-9104-8./
  5. Kozachok, Marina (2012). Perfect prismatoids and the conjecture concerning with face numbers of centrally symmetric polytopes. Yaroslavl International Conference "Discrete Geometry" dedicated to the centenary of A.D.Alexandrov (Yaroslavl, August 13-18, 2012). P.G. Demidov Yaroslavl State University, International B.N. Delaunay Laboratory. с. 46–49..
  6. Reisner, S. (1991). Certain Banach spaces associated with graphs and CL-spaces with 1-unconditional bases. Journal of the London Mathematical Society. Second Series 43 (1): 137–148. MR 1099093. doi:10.1112/jlms/s2-43.1.137..
  7. Martini, H.; Swanepoel, K. J.; de Wet, P. Oloff (2009). Absorbing angles, Steiner minimal trees, and antipodality. Journal of Optimization Theory and Applications 143 (1): 149–157. MR 2545946. arXiv:1108.5046. doi:10.1007/s10957-009-9552-1..
  8. Kim, Jaegil (2014). Minimal volume product near Hanner polytopes. Journal of Functional Analysis 266 (4): 2360–2402. MR 3150164. arXiv:1212.2544. doi:10.1016/j.jfa.2013.08.008..
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.