Побудова Вітгоффа

Побудова Вітгоффа, або конструкція Вітгоффа[1] — метод побудови однорідних многогранників або мозаїк на площині. Метод названо за ім'ям математика В. А. Вітгоффа. Часто метод побудови Вітгоффа називають калейдоскопною побудовою.

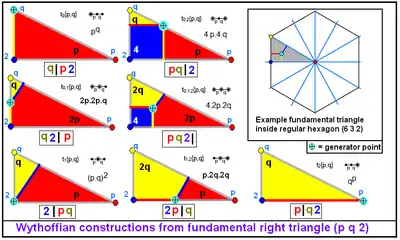
Побудови Вітгоффа з трьома дзеркалами, що утворюють прямокутний трикутник.

Побудова

Побудова ґрунтується на ідеї мозаїк на сфері з використанням сферичних трикутників — див. трикутники Шварца. Ця побудова використовує відбиття відносно сторін трикутника подібно до калейдоскопа. Проте, на відміну від калейдоскопа, відбиття не паралельні, а перетинаються в одній точці. Багаторазові відбиття утворюють кілька копій трикутника. Якщо кути сферичного трикутника вибрано правильно, трикутники покривають сферу мозаїкою один або більше разів.

Якщо помістити точку у відповідне місце всередині сферичного трикутника, оточеного дзеркалами, можна досягти, щоб відбиття цієї точки дали однорідний многогранник. Для сферичного трикутника ABC є чотири позиції, які дають однорідний многогранник:

  1. Точка розташована у вершині A. Вона дає многогранник зі символом Вітгоффа a|b c, де a дорівнює π, поділеному на кут трикутника при вершині A. Аналогічно для b і c.
  2. Точка розташована на відрізку AB в основі бісектриси кута при вершині C. Вона дає многогранник зі символом Вітгоффа a b|c.
  3. Точка розташована в інцентрі трикутника ABC. Вона дає многогранник зі символом Вітгоффа a b c|.
  4. Точка розташована так, що при обертанні її навколо вершин трикутника на подвоєний кут при цих вершинах вона переміщається на однакову відстань. Використовуються лише парні відбиття. Многогранник має символ Вітгоффа |a b c.

Процес, у загальному випадку, застосовується і для отримання правильних політопів у просторах вищих розмірностей, зокрема 4-вимірні однорідні політопи.

Приклади


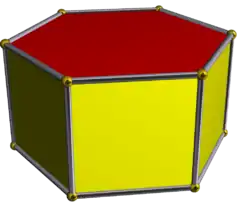Шестикутна призма будується як із сімейства (6 2 2), так і з сімейства (3 2 2).
Зрізана квадратна мозаїка будується за допомогою двох різних позицій у сімействі (4 4 2).

Невітгоффова побудова

Однорідні многогранники, які не можна побудувати за допомогою дзеркальної побудови Вітгоффа, називають невітгоффовими. Їх, у загальному випадку, можна отримати з вітгоффових побудов або альтернацією (видалення вершин через одну) або вставленням чергованих рядів деяких фігур. Обидва типи таких фігур мають обертальну симетрію. Іноді вважають вітгоффовими многогранники, отримані зрізанням вершин, навіть якщо їх можна отримати альтернацією зрізаних з усіх боків фігур.

Приклади
Шестикутна антипризма будується за допомогою альтернації дванадцятикутної призми. Подовжена тикутна мозаїка будується чергуванням рядків квадратної мозаїки і трикутної мозаїки. Великий біромбоікосододекаедр — єдиний невітгоффів однорідний многогранник.

Див. також
  • Символ Вітгоффа — символ для побудови Вітгоффа однорідних многогранників і однорідних паркетів.
  • Діаграми Коксетера — Динкіна — узагальнений символ для побудови Вітгоффа однорідних многогранників і стільників.

Примітки
  1. Веснин, 2017.

Література
  • H. S. M. Coxeter. Chapter 5: The Kaleidoscope, Section: 5.7 Wythoff's construction // Regular Polytopes. — Dover edition, 1973. — ISBN 0-486-61480-8.
  • Coxeter. Chapter 3: Wythoff's Construction for Uniform Polytopes // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — ISBN 978-0-486-40919-1.
  • Har'El, Z. Uniform Solution for Uniform Polyhedra // Geometriae Dedicata. — 1993. — № 47 (7 грудня). — С. 57—110. Архівовано з джерела 15 липня 2009. Section 4: The Kaleidoscope.
  • W.A. Wythoff. A relation between the polytopes of the C600-family // Proceedings of the Section of Sciences. — Koninklijke Akademie van Wetenschappen te Amsterdam, 1918. — № 20 (7 грудня). — С. 966—970.
  • А. Ю. Веснин. Прямоугольные многогранники и трехмерные гиперболические многообразия. — УМН. — 2017. — С. 147–190.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.