Полюс і поляра

У геометрії, полюс і поляра є відповідно точка та пряма, які перебувають в унікальному відношенні відносно певного конічного перетину.

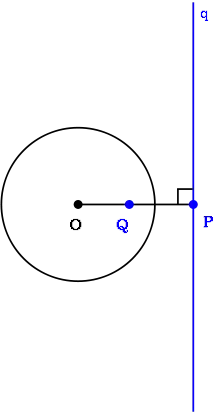
Поляра q до точки Q відносно кола радіуса r з центром у точці O. Точка P є точкою інверсії до Q; поляра — це пряма, яка проходить через P і перпендикулярна до прямої, яка проходить через O, P і Q.

Для певного кола, взаємність у колі означає перетворення кожної точки на площині у її поляру та кожної прямої на площині у її полюс.

Характеристики

Полюси та поляри мають декілька корисних характеристик:

Якщо точка P лежить на прямій l, тоді полюс L прямої l лежить на полярі p точки P.
Якщо точка P рухається вздовж прямої l, її поляра p обертається навколо полюса L прямої l.
Якщо з полюса до конічного перетину можна провести дві дотичні прямі, тоді його поляра проходить через обидві точки дотику.
Якщо точка лежить на конічному перетині, її поляра є дотичною в цій точці до конічного перетину.
Якщо точка P лежить на власній полярі, то P розташована на конічному перетині.
Кожна лінія має, відносно невиродженого конічного перетину, лише один полюс.

Окремі випадки кіл

Полюсом прямої L у колі C є точка P, яка є інверсією у колі C точки Q на L, яка найближча до центру кола. І навпаки, полярна лінія (або поляра) точки P відносно кола C є лінією L, такою, що її найближча до центра кола точка Q є інверсією точки P у C.

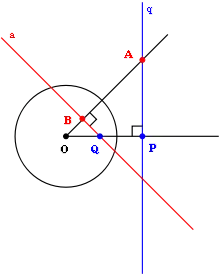
Якщо точка A лежить на полярі q іншої точки Q, тоді Q лежить на полярі a точки A. Більш загально, поляри всіх точок на лінії q повинні проходити через її полюс Q.

Відношення між полярами і полюсами є взаємними. Тобто, якщо точка A лежить на полярі q іншої точки Q, тоді Q повинна лежати на полярі a точки A. Дві полярні лінії a і q не обов'язково є паралельними.

Є інший опис полярної лінії точки P у випадку, коли вона лежить за межами кола C. У цьому випадку, через P проходять дві прямі, які є дотичними до кола, і поляра точки P є лінією, що проходить через дві точки дотику. Це показує, що поляра та полюс є концепціями площини у проєктивній геометрії і узагальнюються на будь-який несингулярний конічний перетин замість кола C.

Взаємність і проєктивна дуальність

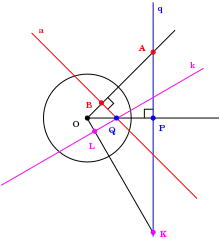
Ілюстрація дуальності між точками та лініями, та подвійного значення «інцидентність». Якщо дві лінії a і k проходять через одну точку Q, тоді поляра q точки Q з'єднує полюси A і K ліній a і k, відповідно.

Концепції полюса та його полярної лінії отримали розвиток у проєктивній геометрії. Наприклад, полярна лінія може розглядатись як набір проєктивних гармонійних сполучених точок для заданої точки (полюса) відносно конічного перетину. Операція заміни кожної точки її полярною лінією і навпаки відома як полярність.

Полярність — це кореляція, яка також є інволюцією.

Загальні конічні перетини

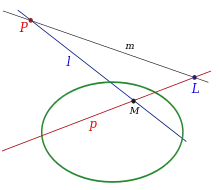
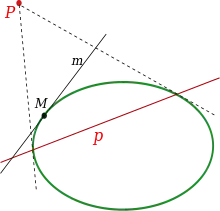
Лінія p є полярою для точки P, l до L і m до M

p є полярною лінією до точки P ; m є полярною лінією до M

Концепції полюса, поляри і взаємність можна узагальнити з кіл на інші конічні перетини: еліпс, гіперболу й параболу. Це узагальнення можливе, оскільки конічні перетини є результатом взаємності кола в іншому колі, а пов'язані характеристики, такі як інцидентність та подвійне відношення, зберігаються за всіх проєктивних перетворень.

Розрахунок поляри до точки

Конічний перетин можна задати як рівняння другого ступеня у декартовій системі координат (x, y) площини

A_{xx}x^{2}+2A_{xy}xy+A_{yy}y^{2}+2B_{x}x+2B_{y}y+C=0\,

де A_xx, A_xy, A_yy, B_x, B_y і C є сталими, які визначають рівняння. Для такого конічного перетину, полярна лінія до заданої точки (полюса) (ξ, η) визначається рівнянням

Dx+Ey+F=0\,

де D, E і F така само є сталими, які залежать від координат полюса (ξ, η)

{\begin{aligned}D&=A_{xx}\xi +A_{xy}\eta +B_{x}\\E&=A_{xy}\xi +A_{yy}\eta +B_{y}\\F&=B_{x}\xi +B_{y}\eta +C\,\end{aligned}}

Розрахунок полюса прямої

Полюс прямої $Dx+Ey+F=0$ , відносно невиродженого конічного перетину

A_{xx}x^{2}+2A_{xy}xy+A_{yy}y^{2}+2B_{x}x+2B_{y}y+C=0\,

можна розрахувати за два кроки.

Спочатку розраховуються числа x, y і z з

{\begin{bmatrix}x\\y\\z\end{bmatrix}}={\begin{bmatrix}A_{xx}&A_{xy}&B_{x}\\A_{xy}&A_{yy}&B_{y}\\B_{x}&B_{y}&C\end{bmatrix}}^{-1}\cdot {\begin{bmatrix}D\\E\\F\end{bmatrix}}

Тоді полюс — це точка з координатами $\left({\frac {x}{z}},{\frac {y}{z}}\right)$

Застосування

Полюси та поляри визначив Ж. Жергонн та використав для розв'язання задачі Аполлонія.[1]

У площинній динаміці полюс є центром обертання, поляра — лінією дії сили, а конічний перетин є матрицею маса-інерція.[2] Це відношення полюс-поляра використовується для визначення центру удару плоского твердого тіла. Якщо полюс є центром обертання, тоді поляра є лінією удару як описано в площинному гвинтовому численні.

Див. також

Джерела

Johnson RA (1960). Advanced Euclidean Geometry: An Elementary treatise on the geometry of the Triangle and the Circle. New York: Dover Publications. с. 100–105.
Coxeter HSM, Greitzer SL (1967). Geometry Revisited. Washington: MAA. с. 132–136, 150. ISBN 978-0-88385-619-2.
Gray J J (2007). Worlds Out of Nothing: A Course in the history of Geometry in the 19th century. London: Springer Verlag. с. 21. ISBN 978-1-84628-632-2.
Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. с. 43–45. LCCN 59014456. The paperback version published by Dover Publications has the ISBN 978-0-486-41147-7.
Wells D (1991). The Penguin Dictionary of Curious and Interesting Geometry. New York: Penguin Books. с. 190–191. ISBN 0-14-011813-6.

Примітки

Apollonius’ Problem: A Study of Solutions and Their Connections. Процитовано 4 червня 2013.
John Alexiou Thesis, Chapter 5, pp. 80–108 Архівовано 2011-07-19 у Wayback Machine.

Посилання

Інтерактивна анімація з численними полярами і полюсами на Cut-the-Knot
Інтерактивна анімація з одним полюсом та його полярою
Interactive 3D with coloured multiple poles/polars — open source
Weisstein, Eric W. Поляра(англ.) на сайті Wolfram MathWorld.
Weisstein, Eric W. Взаємність(англ.) на сайті Wolfram MathWorld.
Weisstein, Eric W. Інверсійний полюс(англ.) на сайті Wolfram MathWorld.
Weisstein, Eric W. Reciprocal curve(англ.) на сайті Wolfram MathWorld.
Tutorial at Math-abundance

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Apollonius’ Problem: A Study of Solutions and Their Connections. Процитовано 4 червня 2013.

[2] John Alexiou Thesis, Chapter 5, pp. 80–108 Архівовано 2011-07-19 у Wayback Machine.