Проєкція Меркатора
Рівнокутна циліндрична проєкція Меркатора — одна з основних картографічних проєкцій. Розроблена Герардом Меркатором для застосування в його «Атласі».
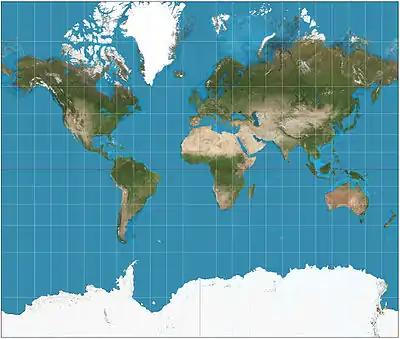

«Рівнокутна» в назві проєкції підкреслює те, що проєкція зберігає кути між напрямками. Всі локсодроми в ній зображуються прямими лініями. Меридіани в проєкції Меркатора представляються паралельними рівновіддаленими лініями. Паралелі ж являють собою паралельні лінії, відстань між якими дорівнює відстані між меридіанами в районі екватора і швидко збільшується при наближенні до полюсів. Самі полюси не можуть бути зображені на проєкції Меркатора (вони відповідають особливості функції, що відображає координати на сфері координатами на площині), тому зазвичай карту в проєкції Меркатора обмежують областями до 80-85° градусів північної і південної широти.
Масштаб на карті в цій проєкції не є постійним, він збільшується від екватора до полюсів (як зворотний косинус широти), однак масштаби по вертикалі і по горизонталі завжди рівні, чим, власне, і досягається рівнокутність проєкції. На картах в даній проєкції завжди вказується, до якої паралелі відноситься основний масштаб карти.
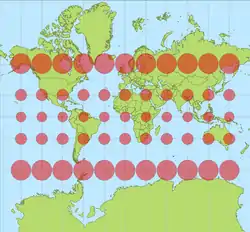
Оскільки проєкція Меркатора має різний масштаб на різних ділянках, ця проєкція не зберігає площі. Якщо основний масштаб відноситься до екватора, то найбільші спотворення розмірів об'єктів будуть біля полюсів. Це добре помітно на мапах у цій проєкції: на них Гренландія здається в 2-3 рази більшою від Австралії і порівнянна за розмірами з Південною Америкою. У реальності Гренландія втричі менша від Австралії і у 8 разів менша від Південної Америки.
Проєкція Меркатора виявилася досить зручною для потреб мореплавства, особливо в давні часи. Пояснюється це тим, що траєкторія руху корабля, що йде під одним і тим же румбом до меридіану (тобто з незмінним положенням стрілки компаса щодо шкали) зображається прямою лінією на карті в проєкції Меркатора.
Математичне представлення проєкції Меркатора
Для початку розглянемо найпростіший варіант проєкції Меркатора: проєкцію сфери на циліндр. Цей варіант не враховує сплюснутість Землі біля полюсів. Циліндричність проєкції відразу дає нам вираз для горизонтальної координати на карті: вона просто пропорційна довготі точки (при використанні в розрахунках слід врахувати, що представлятися ця величина повинна в радіанах)
- .
Умова рівнокутності — це просто рівність масштабів по горизонтальній та вертикальній осі. Оскільки масштаб по осі X на широті рівний просто (R — радіус Землі), то з умови ми одержуєм вираз для залежності y від
- .
Зворотне перетворення
Тепер неважко отримати вирази для рівнокутної проєкції з урахуванням еліпсоїдальної форми Землі. Для цього треба записати метричну форму для еліпсоїда (a — велика піввісь, b — менша) в географічних координатах
перейти в ній до координат x та y і прирівняти масштаби по осях. Після дещо марудного інтегрування одержуєм
Тут — ексцентриситет земного еліпсоїда. Зворотне перетворення не виражається в елементарних функціях, але рівняння для зворотного перетворення легко розв'язати методом теорії збурень за малим .
Ітераційна формула для зворотного перетворення має такий вигляд:
- , де можна взяти рівним 0 або приблизно розрахувати за формулою для сфероїда.
