Рівнобедрений прямокутний трикутник

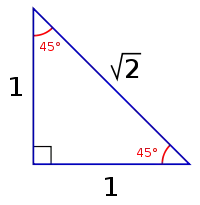
Рівнобедрений прямокутний трикутник — це особливий випадок рівнобедреного і прямокутного трикутника, у якому внутрішній кут дорівнює 45°:

\alpha =\beta =45^{\circ }={\frac {\pi }{4}}\!\,,

Описане та вписане коло у рівнобедреному прямокутному трикутнику. Відстань між центрами кіл однакова

d=r\,

.

Рівнобедрений прямокутний трикутник і рівнобедрений трикутник з рівними описаним і вписаним колом і однаковій відстані між їх центрами

d=r\,

.

третій внутрішній кут є прямим:

\gamma =180^{\circ }-2\alpha =90^{\circ }={\frac {\pi }{2}}\!\,,

так що внутрішні кути відносяться як 1 : 1 : 2.

Бічні сторони трикутника дорівнюють:

a=b={\frac {c{\sqrt {2}}}{2}}\!\,,

основа дорівнює:

c=a{\sqrt {2}}\!\,,

тому сторони відносяться як 1 : 1 : √2. Бічні сторони є катетами, основа є гіпотенузою.

Чотири таких трикутники утворюють квадрат, у яких основа така ж, як квадрат площі. Якщо основа дорівнює діагоналі квадрата, то квадрат складається з двох таких трикутників.

Висота, проведена до гіпотенузи, дорівнює її половині:

v_{c}={\frac {a{\sqrt {2}}}{2}}={\frac {c}{2}}=R\!\,,

де R — радіус описаного кола.

У евклідовій геометрії трикутники з такими внутрішніми кутами є єдиними можливими трикутниками, які є одночасно прямокутними і рівнобедреними. У сферичній та гіперболічній геометрії існує нескінченно багато форм прямокутного рівнобедреного трикутника.

Периметр

Периметр рівнобедреного прямокутного трикутника:

P=a+b+c=a(2+{\sqrt {2}})\!\,.

Площа

Площа рівнобедреного прямокутного трикутника:

S={\frac {a^{2}}{2}}={\frac {c^{2}}{4}}\!\,.

Площу рівнобедреного прямокутного трикутника можна подати за допомогою формули Герона:

S={\sqrt {p(p-a)^{2}(p-a{\sqrt {2}})}}\!\,,

де p — півпериметр рівнобедреного прямокутного трикутника:

p={\frac {P}{2}}=a\left(1+{\frac {\sqrt {2}}{2}}\right)\!\,.

Загальні характеристики

Описане і вписане коло

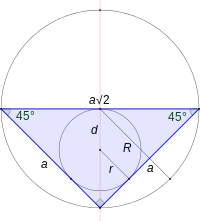
Рівнобедрений прямокутний трикутник, як і всі трикутники, є біцентричним. У ньому:

$r\!\,$	$R\!\,$	$a\!\,$	$c\!\,$
$R\left({\sqrt {2}}-1\right)={\frac {a}{2}}\left(2-{\sqrt {2}}\right)={\frac {c}{2}}\left({\sqrt {2}}-1\right)\!\,$	${\frac {r}{{\sqrt {2}}-1}}={\frac {a}{2}}{\sqrt {2}}={\frac {c}{2}}\!\,$	${\frac {2r}{2-{\sqrt {2}}}}=R{\sqrt {2}}={\frac {c}{2}}{\sqrt {2}}\!\,$	${\frac {2r}{{\sqrt {2}}-1}}=2R=a{\sqrt {2}}\!\,$

Тут r — радіус вписаного кола, R — радіус описаного кола, a — довжина катетів та c — довжина основи рівнобедреного прямокутного трикутника.

Відстань між центрами вписаного та описаного кіл d дорівнює радіусу вписаного кола r і дається рівнянням Ейлера:

d^{2}=R(R-2r)={\frac {a^{2}}{2}}\left(3-2{\sqrt {2}}\right)\!\,

d=r={\frac {a}{2}}\left(2-{\sqrt {2}}\right)=a{\sqrt {{\frac {1}{2}}\left(3-2{\sqrt {2}}\right)}}\approx 0,2928932\,a\!\,.

Рівнобедрений трикутник, що має те саме описане і вписане коло і однакову відстань між їх центрами ( $d=r\,$ ), має кути:

\alpha =\beta =\operatorname {arc\,tg} {\frac {4-{\sqrt {2}}}{{\sqrt {2}}{\sqrt {8{\sqrt {2}}-11}}}}\approx 72,968751^{\circ }\!\,,

\gamma =180^{\circ }-2\alpha \approx 34,062496^{\circ }\!\,.

Теорема Піфагора для рівнобедреного прямокутного трикутника

Квадрат гіпотенузи дорівнює подвоєнному квадрату катета:

$c^{2}=2a^{2}$

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.