Таблиця множення

Таблиця множення (таблиця Піфагора) — математична таблиця, що використовується для визначення операції множення для алгебраїчних систем.

Таблиця множення десяткових чисел вивчається як складова частина елементарної арифметики по всьому світу, оскільки вона закладає фундамент для арифметичних операцій із десятковими числами. Необхідно вивчити таблицю до 9 × 9, або до 12 × 12 аби бути вправним у традиційній математиці. Про винайдення найдавнішого зразка таблиці множення, внаслідок епіграфічних досліджень бамбукового корпусу Цінхуа 清華簡, було оголошено у січні 2014 року. Знахідка датується другою половиною періоду Воюючих Країн (4—3 с. до н. е.).

Історія

Бамбукові дощечки Цінхуа, Китайська таблиця множення десяткових чисел періоду Чжаньго 305 р. до н. е.

Найдавніша відома таблиця множення використовувалася вавілонянами приблизно 4000 років тому[1]. Однак вони користувалися 60-тирічною системою чисел[1]. Найстарішою відомою таблицею множення десяткових чисел є китайська Бамбукова таблиця Цінхуа, що датована приблизно 305 р. до н. е. Вона існувала під час періоду Чжаньго[1].

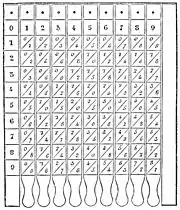
«Таблиця Піфагора» на Палочках Непера[2]

Таблицю множення іноді пов'язують із давньогрецьким математиком Піфагором (570—495 до н. е.). У багатьох мовах світу її називають таблицею Піфагора (наприклад, у французькій, італійський і у нас)[3]. Греко-римський математик Нікомахус (60—120 н. е.), що був послідовником Неопіфагорієнізму, розмістив таблицю множення у своїй роботі «Введення в арифметику», але найстарішою давньогрецькою таблицею множення, що збереглася, є глиняна табличка, яка датується 1-м століттям н. е. Зараз вона зберігається у Британському музеї[4].

В 493 н. е. Вікторій Аквітанський описав таблицю множення в 98 стовпців, у якій наводився (для римських чисел) результат добутку на числа від 2 до 50, а рядки містили «список чисел, починаючи від однієї тисячі, зменшуючись по сотнях до однієї сотні, потім по десятках до десяти, а потім по одиницях до одного, а потім і до дробів до значення 1/144»[5].

Елементарна арифметика

Таблицю множення можна записати у вигляді таблиці, заголовки рядків та стовпчиків якої є множниками, а комірки таблиці містять добутки, отримані в результаті множення заголовків стовпчика та рядка, на яких знаходиться комірка.

×	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
2	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30
3	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45
4	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60
5	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75
6	6	12	18	24	30	36	42	48	54	60	66	72	78	84	90
7	7	14	21	28	35	42	49	56	63	70	77	84	91	98	105
8	8	16	24	32	40	48	56	64	72	80	88	96	104	112	120
9	9	18	27	36	45	54	63	72	81	90	99	108	117	126	135
10	10	20	30	40	50	60	70	80	90	100	110	120	130	140	150
11	11	22	33	44	55	66	77	88	99	110	121	132	143	154	165
12	12	24	36	48	60	72	84	96	108	120	132	144	156	168	180
13	13	26	39	52	65	78	91	104	117	130	143	156	169	182	195
14	14	28	42	56	70	84	98	112	126	140	154	168	182	196	210
15	15	30	45	60	75	90	105	120	135	150	165	180	195	210	225

Так, наприклад, значення 3 × 6 = 18 знаходиться на перетині 3 та 6.

Таблиця не містить множення на 0, оскільки довільне дійсне число помножене на нуль, дорівнює нулю.

Вісімкові числа

×	1	2	3	4	5	6	7
1	1	2	3	4	5	6	7
2	2	4	6	10	12	14	16
3	3	6	11	14	17	22	25
4	4	10	14	20	24	30	34
5	5	12	17	24	31	36	43
6	6	14	22	30	36	44	52
7	7	16	25	34	43	52	61

Шістнадцяткові числа

×	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
1	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
2	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E
3	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D
4	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C
5	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B
6	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A
7	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69
8	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78
9	9	12	1B	24	2D	36	3F	48	51	5A	63	6C	75	7E	87
A	A	14	1E	28	32	3C	46	50	5A	64	6E	78	82	8C	96
B	B	16	21	2C	37	42	4D	58	63	6E	79	84	8F	9A	A5
C	C	18	24	30	3C	48	54	60	6C	78	84	90	9C	A8	B4
D	D	1A	27	34	41	4E	5B	68	75	82	8F	9C	A9	B6	C3
E	E	1C	2A	38	46	54	62	70	7E	8C	9A	A8	B6	C4	D2
F	F	1E	2D	3C	4B	5A	69	78	87	96	A5	B4	C3	D2	E1

Див. також

Примітки

Jane Qiu (January 7, 2014). Ancient times table hidden in Chinese bamboo strips. Nature News. doi:10.1038/nature.2014.14482.
Wikisource:Page:Popular Science Monthly Volume 26.djvu/467
for example in An Elementary Treatise on Arithmetic by John Farrar
David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics. New York: Dover Publications (a reprint of the 1951 publication), ISBN 0-486-20429-4, pp. 58, 129.
David W. Maher and John F. Makowski. "Literary evidence for Roman arithmetic with fractions". Classical Philology, 96/4 (October 2001), p. 383.

Посилання

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Qiu-1] Jane Qiu (January 7, 2014). Ancient times table hidden in Chinese bamboo strips. Nature News. doi:10.1038/nature.2014.14482.

[2] Wikisource:Page:Popular Science Monthly Volume 26.djvu/467

[3] r example in An Elementary Treatise on Arithmetic by John Farrar

[4] David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics. New York: Dover Publications (a reprint of the 1951 publication), ISBN 0-486-20429-4, pp. 58, 129.

[5] David W. Maher and John F. Makowski. "Literary evidence for Roman arithmetic with fractions". Classical Philology, 96/4 (October 2001), p. 383.