Ділення

Зовнішні відеофайли
	1. Чому не можна ділити на нуль // Канал «Цікава наука» на YouTube, 9 квітня 2020.

Ді́лення, заст. ділі́ння[1] — у математиці одна з чотирьох базових арифметичних операцій, де іншими є додавання, віднімання і множення. Ділення натуральних чисел — це процес розрахунку кількості, скільки разів одне число міститься в другому числі.[2]^:7 Наприклад, на малюнку праворуч 20 яблук розділено на чотири групи по п'ять яблук, це означає, що двадцять розділене на п'ять дорівнює чотири, або чотири є результатом ділення двадцяти на п'ять. Це позначається як $20 / 5 = 4$ , $20 \div 5 = 4$ , або $205 = 4$ .[3]

20\div 4=5

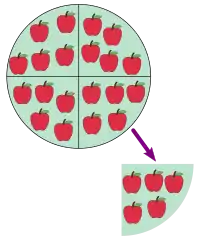
Ділення має два операнди:

ділене — число (чи математичний об'єкт), який ділять;
дільник — число (чи математичний об'єкт) на який ділять.

Результат ділення називається часткою.

При діленні потрібно знайти таку частку $~x$ , яка при множенні на дільник $~b$ дала б ділене $~a$ .

\ x=a/b\quad \iff \quad x\cdot b=a.

Ділення чисел позначають:

двокрапкою $\ 6:3=2,$
знаком $\ 6\div 3=2,$
косою рискою $\ 6/3=2,$
або дробом ${\frac {6}{3}}=2,$ в чисельнику якого записують ділене, а в знаменнику — дільник.

Ділення — бінарна операція, що обернена множенню; якщо $a \times b = c$ , тоді $a = c \div b$ , за умови що $b$ не є нулем. Ділення на нуль для дійсних чисел і в більшості інших випадків є невизначеним,[4]^:246 оскільки, якщо $b = 0$ , тоді $a$ не можна отримати із $b$ і $c$ , оскільки тоді $c$ завжди дорівнюватиме нулю не залежно від $a$ .

Розрахунок

Методи ділення вручну

Ділення як правило пояснюють як процедуру розділення множини об'єктів, наприклад яблук, на деяку задану кількість частин. Розділення об'єктів по одному повторюючи процедуру по колу призводить до методу «віднімання часток», тобто, ділення виконується за допомогою повторюваних кроків віднімання.

Більш систематично і ефективно, але в той же час більш формалізовано і основане на правилах, людина, яка знає таблицю множення може поділити два цілих числа за допомогою розрахунків на папері використовуючи метод короткого ділення, якщо дільник є простим числом. Для більших значень дільників застосовують процедуру ділення стовпчиком. Якщо частка має дробову частину (заданою у вигляді десяткового дробу), алгоритм ділення можна продовжити і розрахувати необхідну кількість значень після коми. Якщо дільник має дробову частину, для виконання розрахунку можна перемістити знак коми праворуч, так що дільник стане цілим числом і виконати розрахунок як для цілих чисел.

Ділення можна розрахувати за допомогою рахівниці перемістивши необхідне число декілька разів, а потім підрахувати кількість зсувів в результаті.

Для ділення двох чисел можна застосувати логарифмічні таблиці, віднявши логарифми двох чисел, а потім знайшовши логарифм результату віднімання.

За допомогою комп'ютера

Сучасні комп'ютери розраховують операцію ділення за допомогою методів, що є швидшими ніж метод довгого ділення. Наприклад, Ділення із залишком, див. алгоритми ділення.

У модульній арифметиці (модуль простого числа) і для дійсних чисел, ненульові числа мають обернене за модулем число. В таких випадках, ділення на число $x$ можна розрахувати як добуток на обернене число $x$ . Цей підхід як правило є самим ефективним.

Властивості

Ділення є дистрибутивною справа для операцій додавання і віднімання. Це означає:

{\frac {a+b}{c}}=(a+b)\div c={\frac {a}{c}}+{\frac {b}{c}}

так само як і при множенні $(a+b)\times c=a\times c+b\times c$ . Але ділення не є дистрибутивним зліва, тобто

{\frac {a}{b+c}}=a\div (b+c)=\left({\frac {b}{a}}+{\frac {c}{a}}\right)^{-1}\neq {\frac {a}{b}}+{\frac {a}{c}}

на відміну від множення.

Якщо виконується декілька операцій ділення, вони виконуються в порядку як вони записані в рядок зліва направо[5][6], це називається асоціативністю зліва:

a\div b\div c=(a\div b)\div c=a\div (b\times c)=a\times b^{-1}\times c^{-1}

.

Обернений елемент

Результати обчислення
Додавання (+)
1-й доданок + 2-й доданок =	сума
Віднімання (−)
зменшуване − від'ємник =	різниця
Множення (×)
1-й множник × 2-й множник =	добуток
Ділення (÷)
ділене ÷ дільник =	частка
Ділення з остачею (mod)
ділене mod дільник =	остача
Піднесення до степеня
основа степеня^{показник степеня} =	степінь
Обчислення кореня (√)
$показник кореня \sqrt підкореневий вираз$ =	корінь
Логарифм (log)
log_основа(число) =	логарифм

Ділення еквівалентне множенню на обернений елемент:

\ a/b\;=\;a\cdot {\frac {1}{b}}

Таке визначення ділення, зазвичай, застосовують для складних математичних об'єктів.

Ліве та праве ділення

Операція множення для складних математичних об'єктів не завжди є комутативною, тому, рівняння $\ ax=b$ та $\ xa=b$ можуть мати різні розв'язки.

У зв'язку з цим використовуються терміни правого та лівого ділення згідно з розв'язками зазначених рівнянь чи множення зліва / справа на обернений елемент:

\ ax=b\quad \iff \quad x=a^{-1}\cdot b

\ xa=b\quad \iff \quad x=b\cdot a^{-1}

Ділення раціональних чисел

Очевидно, що результат ділення цілого числа на ціле число не завжди буде цілим. Замкнутими відносно ділення є раціональні числа.

Для обчислення ділення раціональних чисел використовують множення на число обернене до дільника:

{p \over q}\div {r \over s}={p \over q}\cdot {s \over r}={ps \over qr}.

Ділення дійсних чисел

Ділення двох дійсних чисел дає в результаті інше дійсне число, коли дільник не 0. Воно буде визначене наступним чином a/b = c тоді і лише тоді, коли a = cb і b ≠ 0.

Ділення на нуль

Ділення будь-якого числа на нуль (коли дільник дорівнює нулю) є невизначеним. Це тому, що множення будь-якого скінченного числа на нуль завжди в результаті дає нуль. Якщо ввести такий вираз у калькулятор, більшість з них напише повідомлення про помилку.

Ділення комплексних чисел

Для того, щоб поділити комплексне число $z_{1}=x_{1}+iy_{1}\,$ на комплексне число $z_{2}=x_{2}+iy_{2}\,$ потрібно записати частку у вигляді дробу, а потім домножити чисельник і знаменник на число спряжене до знаменника

{\frac {z_{1}}{z_{2}}}={\frac {x_{1}+iy_{1}}{x_{2}+iy_{2}}}={\frac {z_{1}\cdot {\bar {z}}_{2}}{z_{2}\cdot {\bar {z}}_{2}}}={\frac {(x_{1}+iy_{1})(x_{2}-iy_{2})}{(x_{2}+iy_{2})(x_{2}-iy_{2})}}={\frac {(x_{1}x_{2}+y_{1}y_{2})+i(x_{2}y_{1}-x_{1}y_{2})}{x_{2}^{2}+y_{2}^{2}}}

Ділення матриць

Для обчислення ділення матриць використовують домножання на матрицю обернену до дільника. А оскільки множення матриць не є комутативним, то можливе праве та ліве ділення. Якщо дільник є виродженою матрицею (тобто, для неї не існує оберненої), то можливе використання псевдооберненої матриці.

Див. також

Примітки

Діління // Словарь української мови : у 4 т. / за ред. Бориса Грінченка. — К. : Кіевская старина, 1907—1909.
Blake, A. G. (1887). Arithmetic. Dublin, Ireland: Alexander Thom & Company.
Weisstein, Eric W. Division(англ.) на сайті Wolfram MathWorld.
Derbyshire, John (2004). Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York City: Penguin Books. ISBN 978-0452285255.
George Mark Bergman: Order of arithmetic operations
Education Place: The Order of Operations

Джерела

Дрозд Ю. А. (1997). Теорія алгебричних чисел. Київ: РВЦ “Київський університет„. с. 82. ISBN 966-594-019-8. (укр.)
Погребиський Й. Б. Арифметика. К., 1953;

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Діління // Словарь української мови : у 4 т. / за ред. Бориса Грінченка. — К. : Кіевская старина, 1907—1909.

[2] Blake, A. G. (1887). Arithmetic. Dublin, Ireland: Alexander Thom & Company.

[mwdiv-3] Weisstein, Eric W. Division(англ.) на сайті Wolfram MathWorld.

[4] Derbyshire, John (2004). Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York City: Penguin Books. ISBN 978-0452285255.

[5] George Mark Bergman: Order of arithmetic operations

[6] Education Place: The Order of Operations