Теорема Бояї — Гервіна

В геометрії теорема Воллеса-Бояї-Гервіна,[1] названа ім'ям Вільяма Воллеса, Фаркаша Бояї і Павла Гервіна, стверджує, що будь-які два простих багатокутника рівної площі є рівноскладеними; тобто можна розрізати на кінцеве число багатокутних шматочків та перегрупувати частини так, щоб отримати другий багатокутник.

За теоремою Уоллеса-Бояї-Гервіна квадрат можна розрізати на частини і скласти в трикутник такої самої площі.

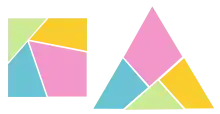
Ясно, що будь-які два рівноскладені багатокутники є рівновеликі.

Перегрупування означає, що можливо застосувати паралельне перенесення і обертання для кожної частини багатокутника.

На відміну від узагальненого рішення для квадратури круга Тарського, аксіома вибору не потрібна для доказу, і розкладання та збирання може бути фактично здійснено фактично, тобто можна все вирізати ножицями з паперу.

Теорему можливо розділити на два кроки. Спершу, кожен багатокутник може бути розрізано на трикутники: для опуклих багатокутників безпосередньо послідовно відрізуємо вершини, для увігнутих багатокутників це робиться більш уважно. Кожен з цих трикутників може потім бути перетворений на прямокутний трикутник, для цього достатньо провести висоту. Тому легко обчислити площу такого трикутника, яка дорівнює половині площі прямокутника, або ж можна розбити прямокутний трикутник і зібрати прямокутник. Другий крок — кожен правильний трикутник (чи еквівалентний прямокутник) може бути перегрупований у прямокутник з заданою (одиничною) довжиною сторони. З цього виходить, що кожен багатокутник може бути еквівалентний прямокутнику з так заданими шириною і висотою, щоб дорівнювати його площі, що і доводить теорему.