Теорема про розділову гіперплощину

В геометрії, теорема про розділову гіперплощину (англ. hyperplane separation theorem) складається з двох варіантів теорем про опуклі множини, які не перетинаються, в $n$ -мірному евклідовому просторі. У першій версії теореми, якщо обидві ці множини замкнені і принаймні одна з них компактна, то існує гіперплощина, яка їх розділяє по двом різним півпросторам, утвореним гіперплощиною, або навіть дві паралельні гіперплощини, що розділені зазором. У другому варіанті, якщо обидві опуклі множини не перетинаються та відкриті, то існує гіперплощина, яка їх розділяє, але ці множини не обов'язково будуть розташовані на ненульовій відстані одна від одної. Вісь, ортогональна до розділової гіперплощини є віссю поділу, коли ортогональні проекції опуклих тіл на вісь не перетинаються.

Ілюстрація до теореми про розділову гіперплощину.

Теорему про розділову гіперплощину досліджував Герман Мінковський. Теорема Гана-Банаха узагальнює результат на випадок топологічних векторних просторів.

Наслідком з цієї теореми є теорема про опорну гіперплощину. В геометрії, максимально розділовою гіперплощиною є гіперплощина, яка відокремлює дві «множини» точок і знаходиться на рівній відстані від обох. Відстань між гіперплощиною і множинами максимальна. Див. статтю про опорні вектори для більш докладної інформації.

Доведення

Нехай A і B дві компактні, закриті, опуклі множини, що не перетинаються. Тоді A і B мають пару близьких точок точок p і q. (функція відстані $d$ (p,B) є неперервною, рівною нулю тільки на B, і на A компактна, вона повинна мати позитивний мінімум p на A.) Тоді будь-яка гіперплощина H, перпендикулярна до сегменту I (p , q) від p до q у внутрішній точці цього сегмента, повинна розділити A з B.

Для другого варіанту теореми, припустимо, що A і B не перетинаються, опуклі і відкриті. Тоді вони можуть бути вичерпані послідовностями компактних, опуклих підмножин A_n і B_n. Перший варіант теореми подає послідовність розділових гіперплощин H_n, яка повинна мати підпослідовність, що сходиться до гіперплощини I. Ця гіперплощина повинна відокремлювати A від B.

Контрприклади і унікальність

Теорема не застосовується, якщо одна з множин не є опуклою.

Якщо одна з множин A або B не є опуклою, то існує безліч можливих контрприкладів для нашої теореми. Наприклад,A і B можуть бути концентричними колами. Більш наочним контрприкладом є випадок, коли множини A і B обидві замкнені, але жодна з них не компактна. Наприклад, якщо A є закритою півплощиною і В обмежена однією гілкою гіперболи, то не існує розділової гіперплощини:

A=\{(x,y):x\leq 0\}

B=\{(x,y):x>0,y\geq 1/x\}.\

(Хоча, в постановці другої теореми, існує гіперплощина, яка відокремлює їх опуклі оболонки.) Інший тип контрприкладів це коли A компактна і B відкрита множина. Наприклад, може бути A — замкнений квадрат і В може бути відкритою площею, яка торкається A.

У першій версії теореми, очевидно, що розділова гіперплощина ніколи не буде єдиною. У другому варіанті, вона може бути єдиною чи їх буде декілька. Технічно, вісь поділу ніколи не єдина, оскільки вона може бути паралельно перенесена; у другому варіанті теореми, вісь поділу може бути єдина з точністю до паралельного перенесення.

Використання для виявлення зіткнень

Теорема про вісь поділу говорить, що:

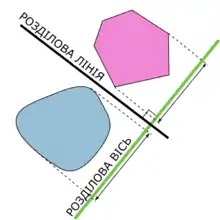
Два опуклі об'єкти не перетинаються, якщо існує лінія (називається вісь), на якій проекції двох об'єктів не перекриваються.

Спираючись на теорему про вісь поділу, можна запропонувати алгоритм для тестування двох опуклих множин на перетин.

Незалежно від вимірності простору, віссю поділу завжди є пряма. Наприклад, в 3D, простори відокремлено площиною, але вісь поділу перпендикулярна розділовій площині.

Теорема про вісь поділу може бути застосована для швидкого виявлення зіткнень між сітками багатокутників. Кожна нормаль до грані чи інше, що задає напрямок для кожної грані використовується як вісь поділу. Зверніть увагу, що це можливо тільки для осі поділу, а не для розділових ліній/площин.

Посилання

Golshtein, E. G.; Tretyakov, N.V.; translated by Tretyakov, N.V. (1996). Modified Lagrangians and monotone maps in optimization. New York: Wiley. с. 6. ISBN 0-471-54821-9.
Shimizu, Kiyotaka; Ishizuka, Yo; Bard, Jonathan F. (1997). Nondifferentiable and two-level mathematical programming. Boston: Kluwer Academic Publishers. с. 19. ISBN 0-7923-9821-1.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.