Формула гаверсинуса

Для будь-яких двох точок на сфері, гаверсинус центрального кута між ними обчислюється за наступною формулою:

${\displaystyle \operatorname {haversin} \left({\frac {d}{r}}\right)=\operatorname {haversin} (\phi _{2}-\phi _{1})+\cos(\phi _{1})\cos(\phi _{2})\operatorname {haversin} (\lambda _{2}-\lambda _{1})}$

де

• haversin це функція гаверсинуса:

${\displaystyle \operatorname {haversin} (\theta )=\sin ^{2}\left({\frac {\theta }{2}}\right)={\frac {1-\cos(\theta )}{2}}}$

• d відстань між двома точками (згідно великого кола сфери; див. відстань на сфері),
• r радіус сфери,
• ${\displaystyle \phi _{1},\phi _{2}}$: широта точки 1 та широта точки 2
• ${\displaystyle \lambda _{1},\lambda _{2}}$: довгота точки 1 and довгота точки 2

Ліворуч від знака рівняння d/r центральний кут у радіанах (пам'ятайте що φ та λ можуть бути переведені з градусів у радіани множенням π/180).

Розв'яжемо для d через застосування зворотного гаверсинуса (якщо можливо), або через використання функції арксинуса (зворотного синуса):

${\displaystyle d=r\operatorname {haversin} ^{-1}(h)=2r\arcsin \left({\sqrt {h}}\right)}$

де h це haversin(d/r), або більш розгорнуто:

${\displaystyle d=2r\arcsin \left({\sqrt {\operatorname {haversin} (\phi _{2}-\phi _{1})+\cos(\phi _{1})\cos(\phi _{2})\operatorname {haversin} (\lambda _{2}-\lambda _{1})}}\right)}$

${\displaystyle =2r\arcsin \left({\sqrt {\sin ^{2}\left({\frac {\phi _{2}-\phi _{1}}{2}}\right)+\cos(\phi _{1})\cos(\phi _{2})\sin ^{2}\left({\frac {\lambda _{2}-\lambda _{1}}{2}}\right)}}\right)}$

Використовуючи цю формулу, переконайтесь що h не перевищує 1 через помилку рухомої коми (d є дійсним лише для h від 0 до 1). h лише наближається до 1 для діаметрально протилежних точок — у цій області відносно багато помилок обчислення мають тенденцію виникнення при використанні кінцевої точності. Оскільки d є великим, (наближається до πR, половини окружності) маленька помилка часто не є головним приводом для турботи у цьому незвичайному випадку (проте існує інша формула відстані на сфері, яка уникає цю проблему). (Формула вище колись написана у термінах функції арктангенса, але потерпає від проблеми h = 1.)^{[джерело?]}

Як описується нижче, схожа формула може бути написана використовуючи косинус (іноді відома як теорема косинусів, не плутайте з теорема косинусів для геометрії на площині) замість гаверсинусів, але якщо 2 точки розташовані близько одна до одної (наприклад <= 1 км) ви можете стикнутись з тим, що cos (d/R) = 0.99999999, що призведе до неточної відповіді. Оскільки формула гаверсинусів використовує синуси це оминає проблему.

Обидві формули лише наближені, якщо взяти до уваги, що Земля не ідеальна сфера: «радіус Землі» R варіюється від 6356,752 км на полюсах до 6378,137 км на екваторі. Більше того, радіус кривої земної поверхні проведеної з півночі на південь на полюсах (≈6399,594 км) на 1% більший ніж на екваторі(≈6335,439 км) — тож формула гаверсинусів та теорема косинусів не можуть бути гарантовано точнішими ніж 0.5%.[4] Більш ефективний метод, що враховує еліптичність Землі запропонований формулою Вінсенти та іншими формулами у статті географічна відстань.

Дано одиничну сферу, «трикутник» на поверхні сфери визначено як з'єднані дугами великих кіл точки u, v, and w на сфері. Якщо довжини цих трьох сторін це a (від u до v), b (від u до w), and c (від v до w), та кут протилежний c це C, тоді теорема гаверсинусів стверджує:

${\displaystyle \operatorname {haversin} (c)=\operatorname {haversin} (a-b)+\sin(a)\sin(b)\,\operatorname {haversin} (C).}$

Оскільки це одинична сфера, довжини a, b, and c є рівними кутам (у радіанах) утвореним цими сторонами з центром сфери (для неодиничних сфер, кожна з цих довжин дуг дорівнює її центральному куту помноженому на радіус сфери).

Сферичний трикутник розв'язаний за теоремою гаверсинусів.

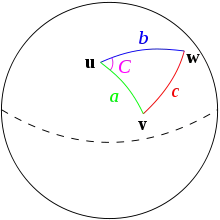
Для отримання формули гаверсинусів попередньої секції з цієї теореми просто розглянемо окремий випадок де u це Північний полюс, коли v та w — це дві точки відстань d між якими нам треба відшукати. У цьому випадку, a та b є π/2 − φ_1,2 (наприклад, 90° − широта), C це відстань за довготою Δλ, та c — це бажаний d/R. Відмітимо, що sin(π/2 − φ) = cos(φ).

Для отримання теореми гаверсинусів, потрібно розпочати зі сферичної теореми косинусів:

${\displaystyle \cos(c)=\cos(a)\cos(b)+\sin(a)\sin(b)\cos(C).\,}$

Як зазначено вище ця формула поганий шлях пошуку c коли c є малим. Замість цього ми замінимо свідчення, що cos(θ) = 1 − 2 haversin(θ), і також застосуємо суму свідчення cos(a − b) = cos(a) cos(b) + sin(a) sin(b), для отримання теореми гаверсинусів вище.

• Сфера Ленарта

• What is the best way to calculate the distance between 2 points? (англ.).
• R. W. Sinnott, «Virtues of the Haversine», Sky and Telescope 68 (2), 159 (1984).
• Deriving the haversine formula, Ask Dr. Math (Apr. 20—21, 1999).
• Romuald Ireneus 'Scibor-Marchocki, Spherical trigonometry, Elementary-Geometry Trigonometry web page (1997).
• W. Gellert, S. Gottwald, M. Hellwich, H. Kästner, and H. Küstner, The VNR Concise Encyclopedia of Mathematics, 2nd ed., ch. 12 (Van Nostrand Reinhold: New York, 1989).
• Реалізація формули гаверсинуса на 16 мовах
• JavaScript implementation of Haversine formula to find distance between two latitude/longitude points.
• C++ implementation of Haversine formula to find distance between two latitude/longitude points.
• Ruby implementation of Haversine formula to find distance between two latitude/longitude points
• Python implementation of Haversine formula to find distance between two latitude/longitude points
• MacOS C implementation of Haversine formula to find distance between two latitude/longitude points using postal zip codes
• Pascal implementation of Haversine formula to find distance between two latitude/longitude points
• Matlab implementation of Haversine formula to find distance between two latitude/longitude points
• MySQL custom UDF function implementation to compute the Haversine formula.