Верхівковий граф
В теорії графів верхівковий граф — це граф, який можна зробити планарним видаленням однієї вершини. Видалену вершину називають верхівкою графу. Зауважимо, що верхівка може бути не одна. Наприклад, у мінімальному непланарному графі K5 або K3,3 кожна вершина є верхівкою. Верхівкові графи включають початково планарні графи, в яких кожна вершина є верхівкою. Нуль-граф вважається також верхівковим, хоча в ньому немає вершин для видалення.
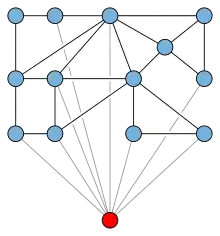
Верхівкові графи замкнуті відносно операції утворення мінорів і грають важливу роль у деяких інших аспектах теорії мінорів графів, таких як незачеплене вкладення[1], гіпотеза Хадвігера[2], YΔY-звідні графи[3] і зв'язок між деревною шириною і діаметром графу[4][5].
Опис і розпізнавання
Верхівкові графи замкнуті відносно операції утворення мінорів — стягування будь-якого ребра або видалення вершини або ребра призводить до іншого верхівкового графу. Дійсно, якщо граф G є верхівковим з верхівкою v, то стягування або видалення, яке не зачіпає вершини v, зберігає планарність решти графу (без вершини v). Це правильно і при видаленні будь-якого ребра, інцидентного v. Якщо стягується ребро, інцидентне v, ефект еквівалентний видаленню протилежного кінця ребра. Якщо ж видаляється сама вершина v, будь-яку іншу вершину можна вважати верхівкою[6].
Оскільки верхівкові графи замкнуті за операцією утворення мінорів, за теоремою Робертсона — Сеймура вони мають характеризацію забороненими графами. Існує лише скінченне число графів, які не є верхівковими графами і не містять як мінор інший граф, який не є верхівковим. Ці графи є забороненими мінорами для властивості «верхівковий граф». Будь-який інший граф G є верхівковим тоді й лише тоді, коли жоден із заборонених мінорів не є мінором графу G. Заборонені мінори включають сім графів з петерсенового сімейства, три незв'язних графи, утворених з об'єднань K5 і K3,3, що не перетинаються, і багато інших графів. Повний список всіх заборонених мінорів залишається незавершеним[6][7].
Попри те, що повний список заборонених мінорів не відомий, є можливість за лінійний час перевірити, чи є даний граф верхівковим, і якщо він такий, знайти верхівку графу. Загальніше, для будь-якої фіксованої константи k можна за лінійний час розпізнати k-верхівкові графи (графи, в яких видалення акуратно вибраної множини, що містить не більше k вершин, приводить до планарного графу[8]). Однак, якщо k не фіксовано, задача стає NP-повною[9].
Хроматичне число
Будь-який верхівковий граф має хроматичне число, яке не перевищує п'яти — планарний граф без верхівки вимагає не більше чотирьох кольорів за теоремою про чотири фарби, а для верхівки достатньо одного додаткового кольору. Робертсон, Сеймур і Томас[2] використовували цей факт для доведення випадку k = 6 гіпотези Хадвігера, твердження, що будь-6-хроматичний граф має повний граф K6 як мінор — вони показали, що будь-який мінімальний контрприклад гіпотезі має бути верхівковим графом, але верхівкових 6-хроматичних графів немає, так що такого контрприкладу не існує.Шаблон:UnsolvedЙоргенсен[10] висловив гіпотезу, що будь-який 6-вершинно -зв'язний граф, що не має мінорів K6, повинен бути верхівковим. Якби це довели, результат Робертсона — Сеймура — Томаса для гіпотези Хадвігера став би прямим наслідком[2]. Гіпотезу Йоргенсена поки не доведено[11]. Однак якщо гіпотеза хибна, вона має лише скінченне число контрприкладів[12].
Локальна деревна ширина
Родина графів F має обмежену локальну деревну ширину, якщо графи з F підпорядковані функціональній залежності між діаметром і деревною шириною — існує функція ƒ, така, що деревна ширина графу з F з діаметром d не перевершує ƒ(d). Верхівкові графи не мають обмеженої локальної деревної ширини — граф, утворений з'єднанням верхівки з кожною вершиною n × n ґратки має деревну ширину n і діаметр 2, так що деревна ширина не обмежена деякою функцією від діаметра цих графів. Проте верхівкові графи тісно пов'язані з графами з обмеженою локальною деревною шириною — замкнуті за мінорами родини графів F, що мають обмежену локальну деревну ширину, є точно сімействами, одним із заборонених мінорів яких є який-небудь верхівковий граф[4][5]. Замкнуті за мінорами родини графів, що мають верхівковий граф як мінор, відомі як вільні від верхівкового мінора. Згідно з цією термінологією зв'язок між верхівковими графами та локальною деревною шириною можна переформулювати так: сімейства графів, вільних від верхівкових мінорів, збігаються з сімействами замкнутих за мінорами графів з обмеженою локальною деревною шириною.
Концепція обмеженої локальної деревної ширини утворює базис теорії двовимірності і дозволяє розв'язувати багато алгоритмічних задач на вільних від верхівкових мінорів графах точно за алгоритмом поліноміального часу, або фіксовано-параметрично розв'язним алгоритмом, або задачу можна наблизити за допомогою схеми наближення до поліноміального часу[4][13][14]. Для вільних від верхівкових мінорів сімейств графів виконується посилена версія структурної теореми графів, що приводить до додаткових апроксимаційних алгоритмів для розфарбовування графів і для задачі комівояжера[15]. Проте деякі з цих результатів можна поширити на довільні замкнуті за мінорами сімейства графів використавши структурні теореми на пов'язані з сімействами вільні від верхівкових мінорів графи[16].
Вкладення
Якщо граф G є верхівковим графом з верхівкою v і дорівнює мінімальному числу граней, необхідних для покриття всіх сусідів верхівки v за планарного вкладення G\{v}, то G можна вкласти у двовимірну поверхню роду додаванням такого числа мостів до планарного вкладення, з'єднавши тим самим усі грані, з якими верхівка v повинна бути з'єднана. Наприклад, додавання однієї вершини до зовніпланарного графу (графу з ) дає планарний граф. Якщо граф G\{v} 3-зв'язний, його межа не відрізняється від оптимальної більше ніж на постійний множник — будь-яке вкладення G в поверхню вимагає роду щонайменше . Однак задача визначення оптимального роду для поверхні вкладення для верхівкових графів є NP-складною задачею[17].
При використанні SPQR-дерев для кодування можливих вкладень планарної частини верхівкового графу, можна обчислити за поліноміальний час укладення графу на площину, в якому перетини викликані тільки ребрами, що виходять з верхівки, і загальне число перетинів мінімальне[18]. Якщо дозволено довільні перетини, задача мінімізації числа перетинів стає NP-складною задачею навіть в особливому випадку верхівкових графів, утворених додаванням одного ребра у планарний граф[19].
Верхівкові графи вклада́нні без зачеплення у тривимірний простір — їх можна вкласти так, що будь-який цикл у графі є межею диска, якого не перетинає будь-яка інша частина графу[20]. Малюнок такого типу можна отримати, намалювавши планарну частину графу на площині, помістивши верхівку графу над площиною, і з'єднавши її з сусідами відрізками. Вкладанні без зачеплень графи утворюють замкнуте за мінорами сімейство з сімома графами з петерсенового сімейства як мінімальними забороненими мінорами[1]. Таким чином, ці графи є забороненими мінорами і для верхівкових графів. Існують, однак, вкладанні без зачеплення графи, які не є верхівковими.
YΔY-звідність
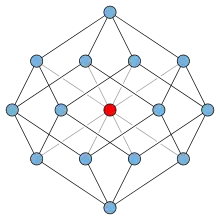
Зв'язний граф є YΔY-звідним, якщо його можна звести до одиничної вершини послідовністю кроків, кожен з яких є Δ-Y або Y-Δ перетворенням, видаленням петлі або кратних ребер, видаленням вершини з одним сусідом і заміною вершини степеня два і двох суміжних ребер одним ребром[3].
Подібно до верхівкових графів і вкладанних без зачеплення графів YΔY-звідні графи замкнуті відносно операції утворення мінорів. Подібно до вкладанних без зачеплення графів YΔY-звідні графи мають мінімальними забороненими мінорами сім графів з петерсенового сімейства, звідки виникає питання, чи не є тільки ці графи забороненими мінорами і чи не збігаються сімейства YΔY-звідних графів і вкладанних без зачеплення графів. Ніл Робертсон, однак, навів приклад верхівкового графу, що не є YΔY-звідним. Оскільки будь-який верхівковий граф вкладанний без зачеплення, це показує, що існують вкладанні без зачеплення графи, які не є YΔY-звідними, а тому існують додаткові заборонені мінори для YΔY-звідних графів[3].
Верхівковий граф Робертсона наведено на малюнку. Його можна отримати з'єднанням верхівки з усіма вершинами степеня три ромбододекаедра або злиттям двох протилежних вершин графу чотиривимірного гіперкуба. Оскільки граф ромбододекаедра планарний, граф Робертсона є верхівковим. Граф не містить трикутників і має мінімальний степінь чотири, так що до нього не можна застосувати будь-яку операцію YΔY-зведення[3].
Майже планарні графи
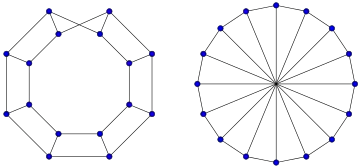
Якщо граф є верхівковим, не обов'язково у нього єдина верхівка. Наприклад, в мінорно мінімальних непланарних графах K5 і K3,3 верхівкою можна вибрати будь-яку вершину. Вагнер[21][22] визначив майже планарний граф як непланарний верхівковий граф, у якому кожна вершина може служити верхівкою. Таким чином, K5 і K3,3 є майже планарними графами. Він дав класифікацію таких графів, розділивши їх на чотири сімейства. Одне сімейство складається з графів, які (подібно драбини Мебіуса) можна вкласти в стрічку Мебіуса таким чином, що край стрічки збігається з гамільтоновим циклом графу. Ще до доведення теореми чотирьох фарб він довів, що будь-який майже планарний граф можна розфарбувати, не перевищивши чотирьох кольорів, за винятком графів, утворених з колеса з непарним зовнішнім циклом заміною центральної вершини двома суміжними вершинами — для такого графу потрібно п'ять фарб. Крім того, він довів, що, за одним винятком (восьмивершинного доповнення куба), будь-який майже планарний граф має вкладення у проєктивну площину.
Проте фраза «майже планарний граф» значною мірою неоднозначна — той самий термін використовувався для верхівкових графів[20][4], графів, утворених додаванням одного ребра до планарного графу[23], графів, утворених з планарного вкладення графу заміною обмеженого числа граней «вихорами» обмеженої шляхової ширини[24], а також деяких інших менш строго визначених множин графів.
Примітки
- Robertson, Seymour, Thomas, 1993b.
- Robertson, Seymour, Thomas, 1993a.
- Truemper, 1992.
- Eppstein, 2000.
- Demaine, Hajiaghayi, 2004.
- Gupta, Impagliazzo, 1991.
- Pierce, 2014.
- Kawarabayashi, 2009.
- Lewis, Yannakakis, 1980.
- Jørgensen, 1994.
- Jorgensen's Conjecture. Open Problem Garden. Процитовано 13 листопада 2016..
- Kawarabayashi, Norine, Thomas, Wollan, 2012.
- Frick, Grohe, 2001.
- Demaine, Hajiaghayi, 2005.
- Demaine, Hajiaghayi, Kawarabayashi, 2009.
- Grohe, 2003.
- Mohar, 2001.
- Chimani, Gutwenger, Mutzel, Wolf, 2009.
- Cabello, Mohar, 2010.
- Robertson, Seymour, Thomas, 1993c.
- Wagner, 1967.
- Wagner, 1970.
- Archdeacon, Bonnington, 2004.
- Abraham, Gavoille, 2006.
Література
- Ittai Abraham, Cyril Gavoille. Proc. 25th ACM Symposium on Principles of Distributed Computing (PODC '06). — 2006. — С. 188–197. — DOI:
- Dan Archdeacon, C.P.C. Paul Bonnington. Obstructions for embedding cubic graphs on the spindle surface // Journal of Combinatorial Theory, Series B. — 2004. — Т. 91, вип. 2 (2 березня). — С. 229–252. — DOI:.
- Sergio Cabello, Bojan Mohar. Proc. 26th ACM Symposium on Computational Geometry (SoCG '10). — 2010. — С. 68–76. — DOI:
- Markus Chimani, Carsten Gutwenger, Petra Mutzel, Christian Wolf. Proc. 20th ACM-SIAM Symposium on Discrete Algorithms (SODA '09). — 2009. — С. 375–383.
- Erik D. Demaine, Mohammad Taghi Hajiaghayi. Diameter and treewidth in minor-closed graph families, revisited // Algorithmica. — 2004. — Т. 40, вип. 3 (2 березня). — С. 211–215. — DOI:.
- Erik D. Demaine, Mohammad Taghi Hajiaghayi. Proc. 16th ACM-SIAM Symposium on Discrete Algorithms (SODA '05). — 2005. — С. 590–601.
- Erik D. Demaine, Mohammad Taghi Hajiaghayi, Ken-ichi Kawarabayashi. Proc. 36th International Colloquium Automata, Languages and Programming (ICALP '09). — Springer-Verlag, 2009. — Т. 5555. — С. 316–327. — (Lecture Notes in Computer Science) — DOI:
- David Eppstein. Diameter and treewidth in minor-closed graph families // Algorithmica. — 2000. — Т. 27, вип. 3 (2 березня). — С. 275–291. — arXiv:math.CO/9907126. — DOI:.
- Markus Frick, Martin Grohe. Deciding first-order properties of locally tree-decomposable structures // Journal of the ACM. — 2001. — Т. 48, вип. 6 (2 березня). — С. 1184–1206. — arXiv:cs/0004007. — DOI:.
- Martin Grohe. Local tree-width, excluded minors, and approximation algorithms // Combinatorica. — 2003. — Т. 23, вип. 4 (2 березня). — С. 613–632. — arXiv:math.CO/0001128. — DOI:.
- A. Gupta, R. Impagliazzo. Proc. 32nd IEEE Symposium on Foundations of Computer Science (FOCS '91). — IEEE Computer Society, 1991. — С. 802–811. — DOI:
- Leif K Jørgensen. Contractions to K8 // Journal of Graph Theory. — 1994. — Т. 18, вип. 5 (2 березня). — С. 431–448. — DOI:.. Как процитировано у Робертсона ((Robertson, Seymour та Thomas, 1993a)).
- Ken-ichi Kawarabayashi. Proc. 50th IEEE Symposium on Foundations of Computer Science (FOCS '09). — IEEE Computer Society, 2009. — С. 639–648. — DOI:.
- Ken-ichi Kawarabayashi, Serguei Norine, Robin Thomas, Paul Wollan. minors in large 6-connected graphs. — 2012. — 2 березня. — arXiv:1203.2192.
- John M. Lewis, Mihalis Yannakakis. The node-deletion problem for hereditary properties is NP-complete // Journal of Computer and System Sciences. — 1980. — Т. 20, вип. 2 (2 березня). — С. 219–230. — DOI:.
- Bojan Mohar. Face covers and the genus problem for apex graphs // Journal of Combinatorial Theory, Series B. — 2001. — Т. 82, вип. 1 (2 березня). — С. 102–117. — DOI:.
- Mike Pierce. Searching for and classifying the finite set of minor-minimal non-apex graphs. — California State University, Chico, 2014. — (Honours thesis)
- Neil Robertson, Paul Seymour, Robin Thomas. Hadwiger's conjecture for K6-free graphs // Combinatorica. — 1993. — Т. 13, вип. 3 (2 березня). — С. 279–361. — DOI:.
- Neil Robertson, Paul Seymour, Robin Thomas. Linkless embeddings of graphs in 3-space // Bulletin of the American Mathematical Society. — 1993. — Т. 28, вип. 1 (2 березня). — С. 84–89. — arXiv:math/9301216. — DOI:..
- Neil Robertson, Paul Seymour, Robin Thomas. Graph Structure Theory: Proc. AMS–IMS–SIAM Joint Summer Research Conference on Graph Minors / Neil Robertson, Paul Seymour. — American Mathematical Society, 1993c. — Т. 147. — С. 125–136. — (Contemporary Mathematics)
- Klaus Truemper. — Academic Press, 1992. — С. 100–101. Архівовано з джерела 29 серпня 2017
- Klaus Wagner. Fastplättbare Graphen // Journal of Combinatorial Theory. — 1967. — Т. 3, вип. 4 (2 березня). — С. 326–365. — DOI:.
- Klaus Wagner. Zum basisproblem der nicht in die projektive ebene einbettbaren graphen, I // Journal of Combinatorial Theory. — 1970. — Т. 9, вип. 1 (2 березня). — С. 27–43. — DOI:.