Властивість розширення гомотопії

Нехай ${\displaystyle X\,\!}$ є топологічним простором і нехай ${\displaystyle A\subset X.}$ Пара просторів ${\displaystyle (X,A)\,\!}$ має властивість розширення гомотопії, якщо, для гомотопії ${\displaystyle f_{t}\colon A\rightarrow Y}$ і неперервного відображення ${\displaystyle F_{0}\colon X\rightarrow Y}$ для якого ${\displaystyle F_{0}|_{A}=f_{0},}$ існує розширення ${\displaystyle F_{t}\colon X\rightarrow Y}$ таке, що ${\displaystyle F_{t}|_{A}=f_{t}.}$

Тобто, пара ${\displaystyle (X,A)\,\!}$ має властивість розширення гомотопії, якщо відображення ${\displaystyle G\colon ((X\times \{0\})\cup (A\times I))\rightarrow Y}$ можна поширити на відображення ${\displaystyle G'\colon X\times I\rightarrow Y}$ (тобто ${\displaystyle G\,\!}$ і ${\displaystyle G'\,\!}$ є рівними там де вони обидва є визначеними).

Якщо пара має таку властивість лише для певного кодомену ${\displaystyle Y\,\!,}$ то кажуть, що ${\displaystyle (X,A)\,\!}$ має властивість розширення гомотопії щодо ${\displaystyle Y\,\!.}$

Властивість розширення гомотопії зображена на наступній схемі:

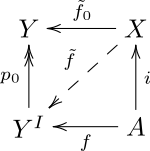
Якщо ця діаграма (без пунктирної стрілки) є комутативною (що еквівалентно умовам, наведеним вище), то пара ${\displaystyle (X,A)}$ має властивість розширення гомотопії, якщо існує відображення ${\displaystyle {\tilde {f}},}$ що робить усю діаграму комутативною. За допомогою каррінга відображення ${\displaystyle {\tilde {f}}\colon X\to Y^{I}}$ відповідає відображенню ${\displaystyle {\tilde {f}}\colon X\times I\to Y.}$

Діаграма вище є двоїстою діаграмі властивості підняття гомотопії. Ця двоїстість називається двоїстістю Екмана-Хілтона.

• Якщо ${\displaystyle X\,\!}$ є клітинним комплексом і ${\displaystyle A\,\!}$ його підкомплексом, то пара ${\displaystyle (X,A)\,\!}$ задовольняє властивість розширення гомотопії.
• Пара ${\displaystyle (X,A)\,\!}$ має властивість розширення гомотопії, тоді і лише тоді коли ${\displaystyle (X\times \{0\}\cup A\times I)}$ є ретрактом ${\displaystyle X\times I.}$

Якщо дана пара має властивість розширення гомотопії, то тотожне відображення ${\displaystyle (X\times \{0\}\cup A\times I)\to (X\times \{0\}\cup A\times I)}$ можна продовжити на деяке відображення ${\displaystyle X\times I\to (X\times \{0\}\cup A\times I).}$ Отже ${\displaystyle (X\times \{0\}\cup A\times I)}$ є ретрактом ${\displaystyle X\times I.}$

Навпаки, якщо існує ретракція ${\displaystyle f:X\times I\to (X\times \{0\}\cup A\times I)}$ то будь-яке відображення ${\displaystyle (X\times \{0\}\cup A\times I)\to Y}$ можна продовжити до відображення ${\displaystyle X\times I\to Y}$ як ${\displaystyle G=g\circ f.}$ Тому пара ${\displaystyle (X,A)\,\!}$ має властивість розширення гомотопії.

• Якщо пара ${\displaystyle (X,A)\,\!}$ має властивість розширення гомотопії і X є гаусдорфовим простором, то A є замкнутою підмножиною простору X.

Справді, якщо ${\displaystyle f:X\times I\to (X\times \{0\}\cup A\times I)}$ є ретракцією, то її образ є також підпростором у ${\displaystyle X\times I}$ для точок якого ${\displaystyle f(z)=z.}$ Оскільки X (а тому і ${\displaystyle X\times I}$) є гаусдорфовим простором то ${\displaystyle X\times \{0\}\cup A\times I}$ є замкнутою підмножиною у ${\displaystyle X\times I,}$ тож A є замкнутою підмножиною простору X.

• Якщо пара ${\displaystyle (X,A)\,\!}$ має властивість розширення гомотопії, то для будь-якого топологічного простору Y пара ${\displaystyle (X\times Y,A\times Y)\,\!}$ теж має властивість розширення гомотопії.
• Якщо пара ${\displaystyle (X,A)}$ має властивість продовження гомотопії і ${\displaystyle A}$ є стягуваним простором, то відображення факторизації ${\displaystyle q\colon X\rightarrow X/A}$ є гомотопною еквівалентністю.

Нехай ${\displaystyle f_{t}:X\to X}$ є гомотопією, що продовжує гомотопію стягнення підпростору A у точку, де ${\displaystyle f_{0}}$ є тотожним відображенням. Оскільки ${\displaystyle f_{t}(A)\subset A,\ \forall t}$ то композиція ${\displaystyle q\circ f_{t}:X\to X/A}$ переправляє A у точку і тому її можна записати також як ${\displaystyle X\xrightarrow {q} X/A\xrightarrow {{\bar {f}}_{t}} X/A}$ і тому можна записати ${\displaystyle q\circ f_{t}={\bar {f}}_{t}\circ q.}$

Для t = 1 за означенням ${\displaystyle f_{1}(A)}$ є точкою до якої стягується A і тому ${\displaystyle f_{1}}$ породжує відображення ${\displaystyle g:X/A\to X}$ для якого ${\displaystyle g\circ q=f_{1}.}$ Також ${\displaystyle q\circ g={\bar {f}}_{1}}$ оскільки ${\displaystyle q\circ g({\bar {x}})=q\circ g\circ q(x)=q\circ f_{1}(x){\bar {f}}_{1}\circ q(x)={\bar {f}}_{1}({\bar {x}}).}$ Відображення g і q є гомотопно оберненими оскільки ${\displaystyle g\circ q=f_{1}\simeq f_{0}}$ через гомотопію ${\displaystyle f_{t}}$ і ${\displaystyle q\circ q={\bar {f}}_{1}\simeq {\bar {f}}_{0}}$ через гомотопію ${\displaystyle {\bar {f}}_{t},}$ а за означеннями ${\displaystyle f_{0}}$ і ${\displaystyle {\bar {f}}_{0}}$ є тотожніми відображеннями на просторах ${\displaystyle X}$ і ${\displaystyle X/A.}$

• Якщо ${\displaystyle (X,A)}$ має властивість розширення гомотопії, то включення ${\displaystyle i\colon A\to X}$ є кофібрацією. Насправді, якщо врахувати будь-яку кофібрацію ${\displaystyle i\colon Y\to Z,}$ то ${\displaystyle \mathbf {\mathit {Y}} }$ є гомеоморфним його образу при відображенні ${\displaystyle \mathbf {\mathit {i}} .}$ Це означає, що будь-яка кофібрація може розглядатися як відображення включення, що має властивість розширення гомотопії.
• Якщо ${\displaystyle (X,A)}$ і ${\displaystyle (Y,A)}$ є парами просторів із властивістю гомотопного продовження і ${\displaystyle f\colon X\to Y}$ є гомотопною еквівалентністю, що є тотожним відображенням на ${\displaystyle A,}$ то ${\displaystyle f}$ є гомотопною еквівалентністю відносно ${\displaystyle A.}$

• Кофібрація

• Hatcher, Allen (2002). Algebraic Topology. Cambridge University Press. ISBN 0-521-79540-0.
• Maunder, Charles Richard Francis (1980). Algebraic topology. Cambridge University Press. ISBN 9780521231619.